The Museum of HP Calculators

Basic Slide Rule Instructions

To multiply two numbers on a typical slide rule, the user set the left index (start of the scale) on the C scale to line up with one factor on the D scale. (All labels refer to Pickett scales. Scale labels were not completely uniform between brands.) The user then found the second factor on the C scale and looked on the D scale for the product. By doing this, the user effectively added the logs (lengths) of the two numbers and looked up the antilog.

Multiplications with more than a single digit were carried out by making use of the smaller graduations to represent additional digits of decreasing significance. The precision available to the user was directly proportional to the size of the device (or the smallest lines the user could resolve.) The slide rule did not indicate the decimal point. That was done by the user - typically by estimation, "common sense" or by computing the characteristic. For example:


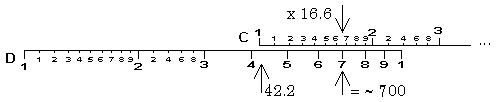
Picture of 42.2 x 16.6 = 700 on a K&E 20" rule (~40K)
Here the result is 7 - estimation of 10x40 and 20x40 makes it obvious that the result is 700. (The 41' cylindrical Fuller model makes it clear that the result is just above 700.5.)

Division was performed by reversing the multiplication steps (setting the divisor on the C scale opposite the dividend on the D scale and reading the result of the D scale under the C scale index.) To multiply multiple numbers, the user simply moved the C index to the previous product to start the next multiplication. (The hairline was handy for keeping a pointer on the previous product while moving the slide.)

There were many other scales. Many were for unary functions which required no sliding. Some common scales were:

CI and DI: Reciprocals
These scales were the reciprocal (1/x) of C and D respectively. The user found the number on C or D and read the reciprocal on CI or DI respectively. For example, placing the hairline on 2 on the C scale, the user could read the reciprocal of 5 (.5) on the CI scale. Of course, the process is reversible since .2 is the reciprocal of 5. There were two scales for convenience.
CF, DF, CIF and DIF: Folded Scales
These scales were "folded" such that instead of having 1 at each end and π in the middle, they started at π, ran up to 1 in the middle, and then went from 1 to π again on the other end. These scales were used to avoid resetting the slide when a problem would otherwise go off the end. For example, if after aligning the index of C with the first factor on D, the second factor on C was off scale, then the user could instead find the second factor on CF and read the result on DF.
A and B: Square/Square Root
These were the squares of the D and C scales respectively. To determine a square root, the user found the number on A and read the root on D. The process was reversed to find a square. The A scale was simply a D scale, reduced to half its length and printed twice. (The magic of logarithms again.)

As with C and D, there was one fixed and one moving square scale. This allowed a square or square root to be easily included in a chained or combined calculation. (e.g., multiplying by the square or square root of a number could be done in a single operation.)

The tricky part was determining which side of the A scale to use. For example, the square root of 1.44 is 1.2 and the square root of 144 is 12 - both of which could be correctly read from the left side of the A scale. However, the user needed to read the square root of 14.4 from the right side of the scale to get the correct answer of ~3.8. The simplest trick was to write the number in standard form (ie n.nnn x 10exp) and use the left side for even powers of 10. (And the resulting exponent was one half the original exponent.) For odd powers of ten, the user shifted the decimal one place to the right and decreased the exponent of ten by one. Then the user used the right side (and again used one half the exponent of ten for the resulting exponent.)

R1 and R2: Square/Square Root
Whereas A and B were the squares of C and D, some rules also added R1 and R2 which were the square root of D. Instead of 2 D scales reduced to half size, the R1 scale was one half a D scale doubled in size and the R2 scale was the second half. This allowed significantly greater precession.
K: Cube/Cube Root
This scale was used for cubes or cube roots. To find a cube root, the user found the number on K and read the cube root on D. The K scale was simply a D scale shrunk and repeated three times - and the user needed to correctly decide which of the three scales to use for any number. This process was similar to the process used on the squaring scales.
L: Common Logarithms
This scale was used to determine the log (base 10) of a number. More precisely, it determined the mantissa of the logarithm and the user determined the characteristic. For example, placing the hairline on the 2 on the D scale, and reading from the L scale showed that the mantissa of the log of 2 is .3. So, the log of 2 is .3, the log of 20 is 1.3, the log of 200 is 2.3 etc. The user also had to remember that when the number was small, the characteristic became negative but the mantissa remained positive. So, to compute the log of .2, the user added -1 to .3 and the result was -0.7. (The process was reversed for antilogs.)

Since this scale was used to read the values of logs, it was not written in log scale but instead had the values 0 - 1 evenly spaced. It was the D scale that was logarithmic. In fact, the L scale was the only non-logarithmic scale that was commonly found on slide rules.

S: Sines and Cosines
Since the sin x = cos(90-x) the same scale was easily used for both sines and cosines. (The angles for both the cosine and sine were typically printed.) The user read the angle of the sine or cosine on the S scale (keeping in mind that sines increased to the left) and read the result from the D scale.
Cos S: Sines and Cosines
A common alternate labeling for the S scale. (See above.)
T: Tangents and Cotangents
The T scale was used with C or CI to find tangents and cotangents. Again, only one scale was needed since tan x = cot(90-x). Also, since tan x = 1/cot x, a single position on the T scale could be read as a tangent or cotangent by looking at C or CI.
ST: Sines and Tangents for Small Angles
A single scale for finding sines and tangents for small angles - typically less than 5.7 degrees. Since sines and tangents are very close in this region, a single scale was used for both.

Log-log Slide Rules

Log-log rules were invented in 1815 and had scales proportional to the log of the log of the number. This allowed the user to calculate xy in a fashion similar to that used for multiplication. (See above.) Log-log rules can be recognized by the many scales starting with "LL".

Unlike the multiplication scales, the log-log scales did not require the user to determine the decimal point. The scales represented a fairly large range of numbers typically from 0.000045 to 22,000.

To raise a number greater than 1.001 to a power, the LL0 - LL3 scales were used. The four scales represented a continuous range of numbers typically from 1.001 at the left end of LL0 to about 22,000 at the right end of LL3. To raise the number X to the power Y, the index of C was set to line up with the number X on whichever LL scale X appeared on. (Again note that the LL scales were not floating point.) Then the user found Y on the C scale and read the result on the same LL scale. Reading the result on the next higher labeled scale would indicate X(Y×10). Reading the result on the next lower labeled scale would indicate X(Y/10) and so on.

For example, setting the index of C to align with 1.4 on LL2 and the hairline on 2 of C, the user could read that 1.42 is 1.96 on LL2, 1.420 is ~840 on LL3, 1.4.2 is 1.0696 on LL1, and 1.4.02 is 1.00675 on LL0. (All of these results were read on a 10" rule.) To raise a number less than .999 to a power, the LL/0 - LL/3 scales were used.
Picture of a K&E 5" Log-log slide rule. (~44K)
Picture of a Geotec 10" Versalog II slide rule. (~100K)

If none of the above rules have enough scales to suit you, try the Pickett N3-ES Powerlog Exponential rule shown below. In addition to the standard log-log scales it added:

This rather wide 10" rule had 32 Scales in all.
Picture of a Pickett 10" Powerlog Exponential slide rule. (~180K)
As above but smaller. (~45K)

If you prefer something simple, try this K&E Beginner's Slide rule. It had just the basics.
Picture of a K&E 10" Beginners slide rule. (~24K)

Back to early models contents
Go on to Large Rules, Complicated Rules & Sectors
Back to slide rule history