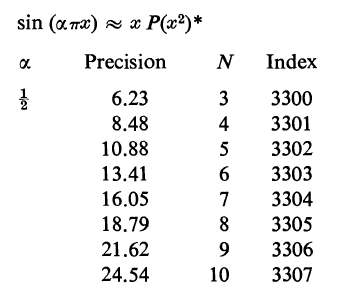
| Re: Hart, 3300 Message #6 Posted by Thomas Klemm on 18 Nov 2013, 6:16 p.m., in response to message #5 by Dieter I finally had a look at the mentioned book from where I copied the Index for the Trigonometric Functions:
* Error criterion: absolute These are the coefficients:
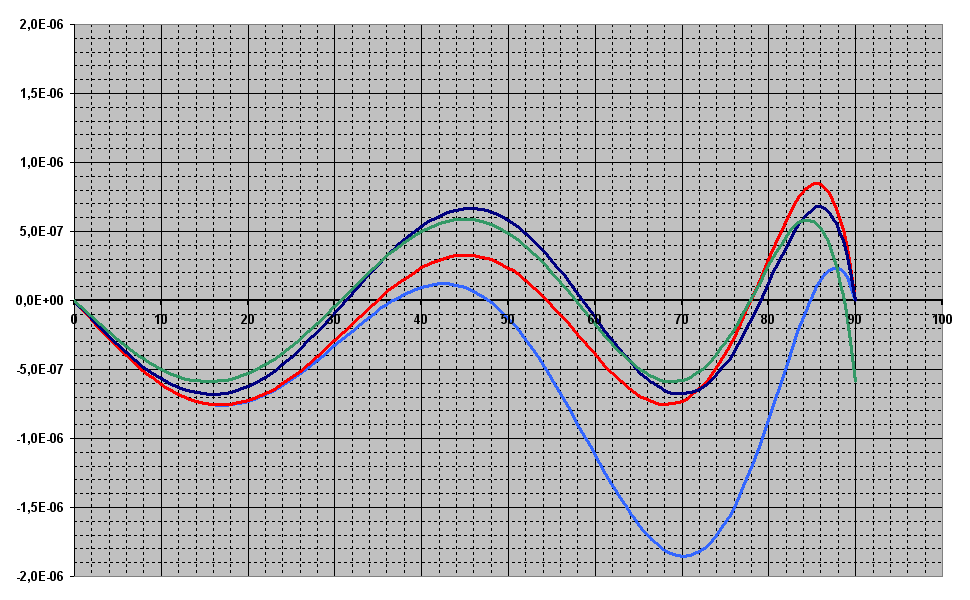
With these more accurate values I got:
x Hart sin(x) |H - s| ------------------------------------- 0 0.0000000 0.0000000 0.000e+00 5 0.0871555 0.0871557 2.832e-07 10 0.1736477 0.1736482 4.972e-07 15 0.2588185 0.2588190 5.881e-07 20 0.3420196 0.3420201 5.303e-07 25 0.4226179 0.4226183 3.337e-07 30 0.5000000 0.5000000 4.471e-08 35 0.5735767 0.5735764 2.623e-07 40 0.6427881 0.6427876 4.997e-07 45 0.7071074 0.7071068 5.891e-07 50 0.7660449 0.7660444 4.864e-07 55 0.8191522 0.8191520 2.048e-07 60 0.8660252 0.8660254 1.717e-07 65 0.9063073 0.9063078 4.930e-07 70 0.9396920 0.9396926 5.799e-07 75 0.9659255 0.9659258 3.071e-07 80 0.9848080 0.9848078 2.502e-07 85 0.9961953 0.9961947 5.838e-07 90 0.9999994 1.0000000 5.891e-07 If I understand you correctly that should match the coefficients of your last post:
Quote: Can you explain why your result doesn't match Hart's solution? Though I didn't check all values it appears that the absolute error is well bellow 6*10-7.
Cheers
#!/usr/bin/python |