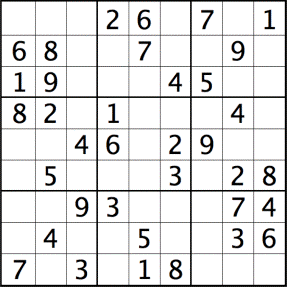
| Re: Optimization questions - HP-15C Message #8 Posted by Thomas Klemm on 29 Oct 2012, 10:30 p.m., in response to message #5 by Marcel Samek The XML-file below can be loaded into the nonpareil emulator so you don't have to type in the program. I was curious how long it would take your program to solve a simple example:
The program is still running.
I'm very much impressed by your effort!
<?xml version="1.0" encoding="ISO-8859-1"?> <!DOCTYPE state SYSTEM "nonpareil.dtd"> <state version="1.00" model="15C" platform="voyager" arch="nut"> <ui/> <chip name="Nut"> <registers> <reg name="a" data="000000fffff000"/> <reg name="b" data="000000fffff000"/> <reg name="c" data="00000000000eae"/> <reg name="m" data="00000000000000"/> <reg name="n" data="00000000000000"/> <reg name="g" data="04"/> <reg name="p" data="c"/> <reg name="q" data="4"/> <reg name="q_sel" data="0"/> <reg name="fo" data="00"/> <reg name="s" data="0800"/> <reg name="pc" data="0000"/> <reg name="stack" index="0" data="006d"/> <reg name="stack" index="1" data="0042"/> <reg name="stack" index="2" data="0000"/> <reg name="stack" index="3" data="0000"/> <reg name="decimal" data="0"/> <reg name="carry" data="0"/> <reg name="awake" data="0"/> <reg name="pf_addr" data="00"/> <reg name="ram_addr" data="007"/> <reg name="active_bank" index="0" data="0"/> <reg name="active_bank" index="1" data="0"/> <reg name="active_bank" index="2" data="0"/> <reg name="active_bank" index="3" data="0"/> <reg name="active_bank" index="4" data="0"/> <reg name="active_bank" index="5" data="0"/> <reg name="active_bank" index="6" data="0"/> <reg name="active_bank" index="7" data="0"/> <reg name="active_bank" index="8" data="0"/> <reg name="active_bank" index="9" data="0"/> <reg name="active_bank" index="a" data="0"/> <reg name="active_bank" index="b" data="0"/> <reg name="active_bank" index="c" data="0"/> <reg name="active_bank" index="d" data="0"/> <reg name="active_bank" index="e" data="0"/> <reg name="active_bank" index="f" data="0"/> </registers> </chip> <chip name="Voyager LCD"> <registers> <reg name="enable" data="1"/> <reg name="blink" data="0"/> </registers> </chip> <memory as="ram"> <loc addr="000" data="00000000000000"/> <loc addr="001" data="00000000000000"/> <loc addr="002" data="00000000000000"/> <loc addr="003" data="00000000000000"/> <loc addr="004" data="000000fffff000"/> <loc addr="005" data="00000000000008"/> <loc addr="006" data="0000000000000c"/> <loc addr="007" data="00000000000eae"/> <loc addr="008" data="00000000000000"/> <loc addr="009" data="2faf8befbe2280"/> <loc addr="00a" data="00000000000000"/> <loc addr="010" data="00000000000000"/> <loc addr="011" data="00000000000000"/> <loc addr="012" data="00000000000000"/> <loc addr="013" data="00000000000000"/> <loc addr="014" data="00000000000000"/> <loc addr="015" data="c0d2d2d2d2d2d2"/> <loc addr="016" data="000000000006e1"/> <loc addr="017" data="00000000000000"/> <loc addr="018" data="00000000000000"/> <loc addr="019" data="00000000000000"/> <loc addr="01a" data="00000000a00000"/> <loc addr="0c0" data="00000000000000"/> <loc addr="0c1" data="00000000000000"/> <loc addr="0c2" data="00000000000000"/> <loc addr="0c3" data="00000000000000"/> <loc addr="0c4" data="00000000000000"/> <loc addr="0c5" data="00000000000000"/> <loc addr="0c6" data="00000000000000"/> <loc addr="0c7" data="00000000000000"/> <loc addr="0c8" data="00000000000000"/> <loc addr="0c9" data="00000000000000"/> <loc addr="0ca" data="00000000000000"/> <loc addr="0cb" data="00000000000000"/> <loc addr="0cc" data="00000000000000"/> <loc addr="0cd" data="00000000000000"/> <loc addr="0ce" data="00000000000000"/> <loc addr="0cf" data="00000000000000"/> <loc addr="0d0" data="00000000000000"/> <loc addr="0d1" data="00000000000000"/> <loc addr="0d2" data="00000000000000"/> <loc addr="0d3" data="00000000000000"/> <loc addr="0d4" data="00000000000000"/> <loc addr="0d5" data="00000000000000"/> <loc addr="0d6" data="00000000000000"/> <loc addr="0d7" data="00000000000000"/> <loc addr="0d8" data="00000000000000"/> <loc addr="0d9" data="00000000000000"/> <loc addr="0da" data="00000000000000"/> <loc addr="0db" data="00000000000000"/> <loc addr="0dc" data="00000000000000"/> <loc addr="0dd" data="00000000000000"/> <loc addr="0de" data="00000000000000"/> <loc addr="0df" data="00000000000000"/> <loc addr="0e0" data="00000000000000"/> <loc addr="0e1" data="00b225faf9c4c4"/> <loc addr="0e2" data="32ff7120f2ebfd"/> <loc addr="0e3" data="30210919ff43ff"/> <loc addr="0e4" data="2d33ff361c7126"/> <loc addr="0e5" data="c3f10c1e2d3619"/> <loc addr="0e6" data="ff52ff29342933"/> <loc addr="0e7" data="293242ff253627"/> <loc addr="0e8" data="faf11c7536f909"/> <loc addr="0e9" data="ff271e713726f1"/> <loc addr="0ea" data="b27531f0f80e41"/> <loc addr="0eb" data="c3f110ff7631f0"/> <loc addr="0ec" data="f82d7137273726"/> <loc addr="0ed" data="f100ff41c3f143"/> <loc addr="0ee" data="ff42ff0ab220f0"/> <loc addr="0ef" data="f1ebfd35862304"/> <loc addr="0f0" data="b24724f8324624"/> <loc addr="0f1" data="f7f13245ccfb33"/> <loc addr="0f2" data="f844fafcf3ebfd"/> <loc addr="0f3" data="f332ebfdf34320"/> <loc addr="0f4" data="f93142ebfdf931"/> <loc addr="0f5" data="81df06b296fafc"/> <loc addr="0f6" data="35fb30368623f7"/> <loc addr="0f7" data="f1324056ef07b2"/> <loc addr="0f8" data="25faf9c49623f6"/> <loc addr="0f9" data="f2c1c5fac353ff"/> <loc addr="0fa" data="30210bb22b342b"/> <loc addr="0fb" data="332b32250db280"/> <loc addr="0fc" data="cdc5f2fbf14005"/> <loc addr="0fd" data="b2c497fa03b286"/> <loc addr="0fe" data="23f6f2c1c101b2"/> <loc addr="0ff" data="b5fca3c5b1fd00"/> </memory> </state>
001 - 42,21, 0 LBL 0 002 - 10 ÷ 003 - 43 36 LASTx 004 - 34 x<>y 005 - 42 44 FRAC 006 - 20 × 007 - 43 34 RND 008 - 43 32 RTN 009 - 42,21, 1 LBL 1 010 - 36 ENTER 011 - 36 ENTER 012 - 2 2 013 - 6 6 014 - 32 3 GSB 3 015 - 45 24 RCL (i) 016 - 43 32 RTN 017 - 42,21, 3 LBL 3 018 - 40 + 019 - 44 25 STO I 020 - 33 R-v 021 - 43 32 RTN 022 - 42,21, 5 LBL 5 023 - 44 0 STO 0 024 - 1 1 025 - 30 - 026 - 2 2 027 - 34 x<>y 028 - 14 y^x 029 - 42, 4, 0 x<> 0 030 - 43 32 RTN 031 - 42,21,14 LBL D 032 - 32 5 GSB 5 033 - 45 2 RCL 2 034 - 32 12 GSB B 035 - 45 3 RCL 3 036 - 32 12 GSB B 037 - 45 4 RCL 4 038 - 32 12 GSB B 039 - 43 32 RTN 040 - 42,21,12 LBL B 041 - 32 1 GSB 1 042 - 45 0 RCL 0 043 - 43, 6, 3 F? 3 044 - 16 CHS 045 - 40 + 046 - 34 x<>y 047 - 36 ENTER 048 - 2 2 049 - 6 6 050 - 32 3 GSB 3 051 - 44 24 STO (i) 052 - 33 R-v 053 - 9 9 054 - 40 + 055 - 32 5 GSB 5 056 - 43 32 RTN 057 - 42,21, 7 LBL 7 058 - 42, 4, 6 x<> 6 059 - 44 0 STO 0 060 - 45 2 RCL 2 061 - 1 1 062 - 7 7 063 - 32 3 GSB 3 064 - 45 24 RCL (i) 065 - 45 6 RCL 6 066 - 45 0 RCL 0 067 - 30 - 068 - 45 5 RCL 5 069 - 20 × 070 - 40 + 071 - 44 24 STO (i) 072 - 43 32 RTN 073 - 42,21, 6 LBL 6 074 - 44,40, 1 STO + 1 075 - 45 1 RCL 1 076 - 9 9 077 - 10 ÷ 078 - 43 44 INT 079 - 44 2 STO 2 080 - 45 1 RCL 1 081 - 9 9 082 - 32 0 GSB 0 083 - 44 3 STO 3 084 - 3 3 085 - 10 ÷ 086 - 43 44 INT 087 - 45 2 RCL 2 088 - 3 3 089 - 10 ÷ 090 - 43 44 INT 091 - 3 3 092 - 20 × 093 - 40 + 094 - 44 4 STO 4 095 - 8 8 096 - 45 3 RCL 3 097 - 30 - 098 - 13 10^x 099 - 44 5 STO 5 100 - 45 2 RCL 2 101 - 1 1 102 - 7 7 103 - 32 4 GSB 4 104 - 44 6 STO 6 105 - 45 2 RCL 2 106 - 8 8 107 - 32 4 GSB 4 108 - 44 7 STO 7 109 - 43 32 RTN 110 - 42,21, 4 LBL 4 111 - 32 3 GSB 3 112 - 45 24 RCL (i) 113 - 45 5 RCL 5 114 - 10 ÷ 115 - 43 44 INT 116 - 1 1 117 - 0 0 118 - 32 0 GSB 0 119 - 43 32 RTN 120 - 42,21,11 LBL A 121 - 43, 5, 2 CF 2 122 - 43, 5, 3 CF 3 123 - 1 1 124 - 16 CHS 125 - 44 1 STO 1 126 - 42,42,.0 LBL .0 127 - 1 1 128 - 32 6 GSB 6 129 - 45 7 RCL 7 130 - 32 7 GSB 7 131 - 45 7 RCL 7 132 - 43,30, 1 TEST 1 133 - 32 14 GSB D 134 - 8 8 135 - 0 0 136 - 45 1 RCL 1 137 - 43,30, 6 TEST 6 138 - 22 .0 GTO .0 139 - 1 1 140 - 16 CHS 141 - 44 1 STO 1 142 - 42,21,15 LBL E 143 - 8 8 144 - 0 0 145 - 45 1 RCL 1 146 - 43,30, 5 TEST 5 147 - 43 32 RTN 148 - 1 1 149 - 32 6 GSB 6 150 - 45 7 RCL 7 151 - 43,30, 1 TEST 1 152 - 22 15 GTO E 153 - 32 7 GSB 7 154 - 42,42,.9 LBL .9 155 - 9 9 156 - 45 6 RCL 6 157 - 43,30, 5 TEST 5 158 - 22 13 GTO C 159 - 1 1 160 - 40 + 161 - 32 7 GSB 7 162 - 45 6 RCL 6 163 - 32 5 GSB 5 164 - 43, 5, 2 CF 2 165 - 45 2 RCL 2 166 - 32 9 GSB 9 167 - 45 3 RCL 3 168 - 32 9 GSB 9 169 - 45 4 RCL 4 170 - 32 9 GSB 9 171 - 43, 6, 2 F? 2 172 - 22 .9 GTO .9 173 - 45 6 RCL 6 174 - 32 14 GSB D 175 - 22 15 GTO E 176 - 42,21,13 LBL C 177 - 1 1 178 - 16 CHS 179 - 32 6 GSB 6 180 - 43,30, 1 TEST 1 181 - 22 13 GTO C 182 - 45 6 RCL 6 183 - 43, 4, 3 SF 3 184 - 32 14 GSB D 185 - 43, 5, 3 CF 3 186 - 22 .9 GTO .9 187 - 42,21, 9 LBL 9 188 - 32 1 GSB 1 189 - 45 0 RCL 0 190 - 10 ÷ 191 - 43 44 INT 192 - 2 2 193 - 32 0 GSB 0 194 - 43,30, 1 TEST 1 195 - 43, 4, 2 SF 2 196 - 33 R-v 197 - 33 R-v 198 - 9 9 199 - 40 + 200 - 32 5 GSB 5 201 - 43 32 RTN |