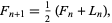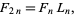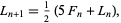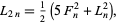Re: RPL programming exercise - One Fibonacci number
Message #33 Posted by Oliver Unter Ecker on 9 Jan 2012, 6:56 p.m.,
in response to message #30 by Oliver Unter Ecker
If you look up the Fibonacci page on wikipedia, you'll see various methods for direct computation of F(n).
One is matrix exponentiation: F(n) = [[0 1][1 1]] ^ n
This program for the 50g will tell you what F(100) mod 10^14 is, for example:
\<< 1.E14 R\->I MODSTO
[[0 1][1 1]] 1.E2 R\->I POWMOD
{1 2} GET
\>>
It takes about 1s on Emu48, so I figure about 10s on a 50g.
Now, if you change 1.E2 to 1.E3 it will produce a negative result. No idea why.
If you try 1.E14 it will tell you: "POWMOD Error: Integer too large"
I conclude that on the 50g POWMOD first does the POW, then the MOD, which, uhm, renders this instruction pretty much useless for matrices. (You want to MOD while you're POW'ing, or else you don't avoid the giant intermediate numbers.)
Well, it works on ND1, and the result is: 88299560546875
Modular matrix exponentiation can be made very fast with the binary method, where you're, essentially, moving in powers of 2 with every iteration. There're only ~50 (~log2(10^14)) matrix multiplications necessary to arrive at 10^14.
This could also be made to work on the 50g with ~10 lines of code to write a proper version of POWMOD. I'm pretty sure this could be made to run in under a minute, for F(10^14).
There's a Project Euler problem (#304) where finding this number (almost this number, there's a different modulus) is the first part of the simple but brutal task of summing up the Fibonacci numbers for each of 100,000 primes following 10^14.
On the 50g, 10 of those primes
\<< 1.E14 R\->I 1 10 START NEXTPRIME NEXT \>>
take about a minute to find (5s in Emulator; not sure how long exactly on the 50g), so 100,000 is a bit... daunting.
(I'm not sure what's done on the 50g, but this speed suggests to me that they're not using Miller-Rabin for the probabilistic primality check that kicks in for large numbers, used by NEXTPRIME.)
Once you have the F(NEXTPRIME(10^14)) and F(PREVPRIME(10^14)), you can use normal Fibonacci iteration (with MOD) to compute the spans between primes and eliminate the need to use matrix exponentiation to find each F(n). With an average of 33 numbers from prime to prime in this range, you're looking at having to compute 3.3 million Fibonacci numbers, though.
If you're interested, here's RPL+ code to do all that:
\<< 1234567891011 =m
1e14 =bias
1e5 =count
\<< [[0 1][1 1]] \->big SWAP
m modpow
DUP {1 1} GET
SWAP {2 1} GET \>> =F2
0 =sum
bias =:prev =a
a F2 EVAL
1 count START
1
a NEXTPRIME =:a prev -
START
DUP ROT +
m MOD
NEXT
a =prev
DUP sum + m MOD =sum
NEXT
DROP DROP
sum
\>>
Note that the matrix exponentiation method actually computes F(n-1), F(n), F(n+1) at once. So, to continue with Fib iteration you can pick two of them from the result matrix, and you're ready to go.
|