The Museum of HP Calculators

HP Forum Archive 18

[ Return to Index | Top of Index ]

x^2 - N*y^2 = 1 (12C)
Message #1 Posted by Gerson W. Barbosa on 17 Jan 2009, 10:41 p.m.

Brahmagupta, an Indian mathematician who lived in the 7th century, presented the following example to one of his theorems:

Find integers x, y such that:

x2 - 92y2 = 1

In his commentary, Brahmagupta added, "a person solving this problem within a year is a mathematician."

(http://en.wikipedia.org/wiki/Indian_mathematics)

I got curious to see how long it would take for us non-mathematicians to solve this problem on the HP-12C. Mine is not here but I tried it on my double-speed HP-15C. The 42-step program, my first attempt, finds the solution in 2 and a half minute. It's an unoptimized version and can be easily ported to the 12C, on which I guess it will find the solution in about five minutes or even less, depending on your approach.

Tip: Follow the link to Pell's equation and see Solution Technique and Example.

More examples: 

   x2 - Ny2 = 1 

   N       x    y

  55       89  12
  60       31   4
  63        8   1

Gerson.

      
Re: x^2 - N*y^2 = 1 (12C)
Message #2 Posted by Gerson W. Barbosa on 18 Jan 2009, 10:42 a.m.,
in response to message #1 by Gerson W. Barbosa

Quote:
it will find the solution in about five minutes or even less, depending on your approach.

As I said, my approach is not optimized. I haven't gone through the continued fraction of sqrt(N) method. As a result of the simple method I have used the running time depends linearly on the value of y solution. For instance, if my estimations are correct, it would take the HP-12C about 3 minutes to find the solution to case N=54 (x=485, y=66) and about 6 months (!) to find the solution for N=97 (x=62809633, y=6377352).

Dario Alpern's Solver can be used to find the solutions:

http://www.alpertron.com.ar/QUAD.HTM

Fill in the boxes with 1, 0, -92, 0, 0 and -1. Step-by-step mode button is worth selecting.

-----------

Uptade:

My second version is 20% faster, which doesn't help so much. The problem consists basically in finding consecutive best rational approximations for sqrt(N). For sqrt(92) only the first 10 of them are needed to find the solution, but my program goes through all other 110 equivalent fractions in between them.

Edited: 18 Jan 2009, 5:05 p.m.

            
Re: x^2 - N*y^2 = 1 (12C)
Message #3 Posted by Brent Hillebrenner on 18 Jan 2009, 7:37 p.m.,
in response to message #2 by Gerson W. Barbosa

Quote:
As I said, my approach is not optimized. I haven't gone through the continued fraction of sqrt(N) method

So you used a brute force method?

                  
Re: x^2 - N*y^2 = 1 (12C)
Message #4 Posted by Gerson W. Barbosa on 18 Jan 2009, 8:59 p.m.,
in response to message #3 by Brent Hillebrenner

Quote:
So you used a brute force method?

A partial brute force method, I'd say. Plain brute force would require about three days to find the fundamental solution to the particular N=92 case on the 12C. The 36-step program does find the solution within four minutes on a normal 15C. An optimized program might solve it under 30 seconds.

Gerson.

                        
Re: x^2 - N*y^2 = 1 (12C) on HP28S
Message #5 Posted by C.Ret on 18 Jan 2009, 10:04 p.m.,
in response to message #4 by Gerson W. Barbosa

The algorithm I had used is composed in two parts :

  • PELL which run the continued fraction until it found the first [x y] interger which match x2-N*y2==1
  • NPELL which compute the successive integer pairs using the recurrent relations xi=xi*x1+N*yi*y1 and yi=xi*y1+yi*x1. 

\<< -> n
   \<< [0 1] [1 0] n \v/ @ initiate [h k]n-2 and [h k]n-1
       DO
          FP             @ store fractional part for futher use
          LAST IP        @ get integer part an
            3 PICK *
           4 ROLL +      @ compute [h k]n=an*[h k]n-1+[h k]n-2
           SWAP
          INV            @ invert fractinal part (stop on error if rational (ex. sqrt(4))
        UNTIL
           OVER          @ get a copy of [h k]n
           ARRY\-> DROP  @ put hn and kn in stack
           SQ n * SWAP SQ
           SWAP – 1 ==   @ test hn2-N*kn2 is 1
        END
        DROP SWAP DROP   @ remove [h k]n-2 and FP from stack
        n SWAP DUP
        NPELL            @ compute second pair using NPELL relation
   \>>
\>>
‘PELL’ STO

\<< \-> n XY1 XYi       
   \<< n                        @ put N on top of stack (lvl 3:)
       XY1                      @ put [x1 y1] on lvl 2:
       XY1 1 GET XYi 1 GET * 
       N XY1 2 GET * XYi 2 GET 
       * +                      @ compute xi+1=x1*xi+N*y1*yi 
       XY1 1 GET XYi 2 GET * 
       XY1 2 GET XYi 1 GET * +  @ compute yi+1=x1*yi+y1*xi 
       {2} \->ARRY              @ build array [xi+1 yi+1]
   \>>
   { PELL NPELL } MENU          @ setup custom menu
\>>
‘NPELL’ STO

Usage:
------
 PELL initiate research and display first and second solution [x1 y1]
 NPELL take n [x1 y1] and [xi yi] from stack to compute [xi+1 yi+1]
                      3:                 n                3:                n
                      2:           [x1 y1]                2:           [x1 y1]
  1: n ---[PELL]--->  1:           [x2 y2] ---[NPELL]---> 1:           [x3 y3] ---[NPELL]--->  ...

Edited: 18 Jan 2009, 10:06 p.m.

                        
Re: x^2 - N*y^2 = 1 (12C)
Message #6 Posted by Brent Hillebrenner on 19 Jan 2009, 11:32 a.m.,
in response to message #4 by Gerson W. Barbosa

Here is my program in Sage Math. I couldn't figure out how you
were getting (a1,a2,a3...an) for the formula, but checking C.ret's
program and taking a second look at "Continued Fractions" on
wikipedia I finally got it. 

By the way... a calculator/handheld preloaded with Sage and with
python scripting would be an awesome machine.

I forget who first brought Sage up on this site, but I've been
having a blast tinkering with it.

Edited Post #1: program breaks down for N = 109 and N = 157 - and
others, I'm sure - because the recursive depth is too large. In
changing the program from a recursive call to a loop, the solution
for N = 109... Well, I'm still waiting!

Edited Post #2: Well, it should only take 20 or 30 iterations to
solve for N = 109 and N = 157... Something else is breaking down.
I printed the output 100 iterations and the algorithm is well past
where the solution should be. A search of the output doesn't bring
up the solution. So, something is amiss with these two numbers.
Anybody??????

------------------------------------------------------------------
The Program
-------------------------------------------------------------------
def pell(N):

    a_n = [pari(sqrt(N)).floor(), pari(sqrt(N)).frac()]
    hk_1 = [1,0]
    hk_2 = [0,1]

    print(N, rcrv_pell(N, a_n, hk_1, hk_2))

def rcrv_pell(N, a_n, hk_1, hk_2):

    hk_n = [a_n[0] * hk_1[0] + hk_2[0], a_n[0] * hk_1[1] + hk_2[1]]
    hk_2 = hk_1
    hk_1 = hk_n
    a_n = [pari(1/a_n[1]).floor(), pari(1.0/a_n[1]).frac()] 

    if hk_1[0]^2 - N * hk_1[1]^2 == 1:
        return hk_1
    else:
        hk_1 = rcrv_pell(N, a_n, hk_1, hk_2)

    return hk_1

-------------------------------------------------------------------
Calling the program
------------------------------------------------------------------

time pell(97)

------------------------------------------------------------------
The output
------------------------------------------------------------------

(97, [62809633, 6377352])
CPU time: 0.01 s,  Wall time: 0.01 s

Edited: 19 Jan 2009, 7:14 p.m.

            
Re: x^2 - N*y^2 = 1 (12C) and 12-digit cut-off
Message #7 Posted by C.Ret on 18 Jan 2009, 9:19 p.m.,
in response to message #2 by Gerson W. Barbosa

Hi,

Since I have no HP-12C, I try the exercise you suggest on my Hp-28S. Using an algorithm based on continued fractions of sqrt(N), I obtain the first [x y] solution of x2-N*y2=1 for the few values of N you give in your post and some more examples I run on my calculator.

The time needed for a HP-28S doesn't exceed a pair of seconds (typically 2.3s to found x=485 y=66 at N=54), which is expected due to technology gab between 12C and 28S.

I observe that I am unable to find any solution for N=94 or N=97. My algorithm seems to run in an endless loop. By breaking the run after a short time (of a few minutes), I observe that the loop go in continued fractions far far away over the expected solutions.

I then realize the stop condition which was simply checking x2-N*y2==1 never occurs with large x or y. Due to the 12-digits floating logic of my calculator, x or y larger than 1E6 may not compare to unity when squared.

Are you sure this is not also append in your algorithm on your 12C ?

  N   time       [x1 y1]          [x2 y2]                [x3 y3]                   [x4 y4]       
---- ------  ---------------------------------------------------------------------------------
   2  0.97s   [    3    2] [       17       12]  [        99        70]  [         577         408]  ...
   3  1.47s   [    2    1] [        7        4]  [        26        15]  [          97          56]  ...
   7  1.72s   [    8    3] [      127       48]  [       204       765]  [       32257       12192]  ...
  17  1.73s   [   33    8] [     2177      528]  [    143649     34840]  [     9478657     2298912]* ...

  50  1.52s   [   99   14] [    19601     2772]  [   3880899    548842]* [   768398401   108667944]* ...
  54  2.30s   [  485   66] [   470449    64020]  [ 456335045  62099334]* [442644523201 60236289960]* ...
  55  2.05s   [   89   12] [    15841     2136]  [   2819609    380196]* [   501874561    67672752]* ...
  60  1.75s   [   31    4] [     1921      248]  [    119071     15372]  [     7380481      952816]* ...
  63  1.50s   [    8    1] [      127       16]  [      2024       255]  [       32257        4064]  ...

  92  2.74s   [ 1151  120] [  2649601   276240]* [6099380351 635904360]* [   1.4040E13   1.4638E12]**...
  93  2.87s   [12151 1260] [295293601 30620520]* [7.17622E12 7.4413E11]**          **           ...
  94  D.N.C         *                                                                          
  95  1.95s   [   39    4] [     3041      312]  [    237159     24332]  [    18495361     1897584]* ...
  96  1.96s   [   49    5] [     4801      490]  [    470449     48015]  [    46099201     4704980]* ...
  97  D.N.C         *                **                                                         
  98  1.80s   [   99   10] [    19601     1980]  [   3880899    392030]* [   768398401    77619960]* ...
  99  1.57s   [   10    1] [      199       20]  [      3970       399]  [       79201        7960]  ...

 255  1.60s   [   16    1] [      511       32]  [     16336      1023]  [      522241       32704]  ...

4097  1.62s   [ 8193  128] [134250497  2097408]*            **                     **           ...
(*) Integer can not be scheck on HP-28S with 12 digits. (**) Intergers cut-off due to 12-digits limits.

The [x2 y2],[x3 y3],... are deduce from the first [x1 y1] (=[x y] obtained from continued fractions loop) using the recurrent relations xi=xi*x1+N*yi*y1 and yi=xi*y1+yi*x1.

Edited: 18 Jan 2009, 9:21 p.m.

                  
Re: x^2 - N*y^2 = 1 (12C) and 12-digit cut-off
Message #8 Posted by Gerson W. Barbosa on 20 Jan 2009, 7:14 a.m.,
in response to message #7 by C.Ret

Quote:
Due to the 12-digits floating logic of my calculator, x or y larger than 1E6 may not compare to unity when squared.

Since the 12C is a 10-digit calculator it will have more constraints regarding this.

I've found a way to determine only the best convergent fractions. Now the 12C program handles N=92 in 17 seconds and N=46 in 27 seconds. I will post my 54 step-program (last GTO 00 included) later.

Regards,

Gerson.

                  
Re: x^2 - N*y^2 = 1 (12C) and 12-digit cut-off
Message #9 Posted by Gerson W. Barbosa on 20 Jan 2009, 11:00 a.m.,
in response to message #7 by C.Ret

HP-12C Program:

01 f 0		19   RCL 2	37   RCL 2
02   STO 0      20   *          38   ENTER
03 g SQRT       21   RCL 5      39   *
04   STO 1      22   +          40   RCL 7
05 g INTG       23   STO 2      41   ENTER
06   STO 2      24   RCL 1      42   *
07 g LASTx      25   /          43   RCL 0
08 g FRAC       26 f RND        44   *
09   STO 3      27   STO 7      45   -
10   1/x        28   RCL 3      46   1
11 g INTG       29   1/x        47   -
12   STO 4      30 g FRAC       48 g X=0
13   1          31   STO 3      49 g GTO 51
14   STO 5      32   1/x        50 g GTO 16
15   STO 7      33 g INTG       51   RCL 7
16   RCL 2      34   STO 4      52   RCL 2
17   STO 6      35   RCL 6      53 f 9
18   RCL 4      36   STO 5      54 g GTO 00


--------------------------------------------

Usage:

92 R/S -> 1151
  x<>y -> 120

--------------------------------------------


  N   time       [x1 y1]          
---- ------  --------------
   2   3.8s   [    3    2] 
   3   3.7s   [    2    1] 
   7   8.1s   [    8    3]
  17   4.9s   [   33    8]
  50   3.9s   [   99   14] 
  54  12.7s   [  485   66]
  55   8.1s   [   89   12]
  60   8.2s   [   31    4]
  63   3.8s   [    8    1]
  92  17.0s   [ 1151  120]
  93  21.3s   [12151 1260]
  94  W.E.T *                                                                        
  95   8.1s   [   39    4] 
  96   8.3s   [   49    5]
  97  W.E.T                                                                   
  98    8.1s  [   99   10] 
  99    3.8s  [   10    1] 
 255    3.9s  [   16    1]
4097    3.9s  [ 8193  128] 

* won't even try :-)

The 12C Platinum (12 digits internally) might handle larger numbers. Also, it will run faster.

Gerson.

            
Re: x^2 - N*y^2 = 1 (12C)
Message #10 Posted by Rodger Rosenbaum on 20 Jan 2009, 7:00 a.m.,
in response to message #2 by Gerson W. Barbosa

Quote:

Dario Alpern's Solver can be used to find the solutions:

http://www.alpertron.com.ar/QUAD.HTM

Fill in the boxes with 1, 0, -92, 0, 0 and -1. Step-by-step mode button is worth selecting.

Try Dario Alpern's Solver with -92 replaced by:

-661
-1621
-19231
-48799
-10003471  (took 1 second)
-40781911  (took 4 seconds)

Edited: 21 Jan 2009, 7:21 p.m.

                  
Re: x^2 - N*y^2 = 1 (12C)
Message #11 Posted by Gerson W. Barbosa on 23 Jan 2009, 5:36 a.m.,
in response to message #10 by Rodger Rosenbaum

Quote:
-40781911 (took 4 seconds)

Intel(R) Core(TM)2Duo CPU @2.66 Ghz: 

-----------

... 738450 683766 821529 349435 839653 (9930 digits)

... 201850 115501 777973 441914 433960 517960 (9934 digits)


Calculation time: 0h 0m 0s

-----------

What Brahmagupta would think of this? :-)

Gerson.

                        
Re: x^2 - N*y^2 = 1 (12C)
Message #12 Posted by Rodger Rosenbaum on 23 Jan 2009, 8:14 a.m.,
in response to message #11 by Gerson W. Barbosa

Did you use Dario's solver running Java on your 2.66 GHz machine, or were you running some other math application?

I got the 4 second time running his Java calculator on an old Pentium III running at 1 GHz.

I'll tell you what Brahmagupta would think. He would think you had made a deal with Satan, because there would be no other way you could solve that problem!!!

                              
Re: x^2 - N*y^2 = 1 (12C)
Message #13 Posted by Gerson W. Barbosa on 23 Jan 2009, 8:34 a.m.,
in response to message #12 by Rodger Rosenbaum

I used Dario's Solver. There was a slight delay before the answer came out, but clearly it took less than half a second. Really impressive!

Gerson.

      
Re: x^2 - N*y^2 = 1 (12C)
Message #14 Posted by MikeO on 20 Jan 2009, 4:25 a.m.,
in response to message #1 by Gerson W. Barbosa

It took approximately 25 seconds using the HP50G.

It seemed to me that a brute force search would go faster by incrementing y by 1 then seeing if we could form a perfect square:

Re-write the equation: x^2 = 1 + 92*y^2 When y=120 we have an answer to the equation given and x=1151

The general case is interesting: x^2 + N*y^2 = 1, where N can be any integer, but it's past my bedtime right now. Perhaps later.

; -MikeO

Here's the not-so-pretty RPL: 

<< 0 1 -> X Y
<< DO 
   Y 2 ^ 92 * 1 + SQRT 'X' STO
   'Y' 1 STO+
   UNTIL X FP 0 ==
   END
   Y 1 -
   X
>>
>>

Edited: 20 Jan 2009, 4:39 a.m.

            
Re: x^2 - N*y^2 = 1 (12C)
Message #15 Posted by MikeO on 20 Jan 2009, 9:03 p.m.,
in response to message #14 by MikeO

Now that I'm a little more awake. I found an interesting thing - that the integer solutions to this problem form a good approximation for the square root of the "N" in the equation. x = 1151, y = 120, and: 1151/120 = 9.591666667, which when squared, is 92.00007. Wow! Cool!

Well, then I decided to read the wikipedia article references and found that this a known feature of the solution and really a deep part of the general solution of the problem.

But, as always, it seems that most problems have been solved. Kind of ruins the fun of looking for solutions sometimes.

-MikeO

                  
Re: x^2 - N*y^2 = 1 (12C)
Message #16 Posted by Gerson W. Barbosa on 21 Jan 2009, 10:02 a.m.,
in response to message #15 by MikeO

Quote:
I found an interesting thing - that the integer solutions to this problem form a good approximation for the square root of the "N" in the equation. x = 1151, y = 120, and: 1151/120 = 9.591666667, which when squared, is 92.00007.

Yes, and the next solutions provived even better approximations:

2649601/276240 = 9.591663047, which matches the square root of 92 (10-digit approximation). See C.Ret's program and table above.

Regards,

Gerson.

      
Re: x^2 - N*y^2 = 1 (12C)
Message #17 Posted by Egan Ford on 21 Jan 2009, 6:18 p.m.,
in response to message #1 by Gerson W. Barbosa

Hello Gerson, here is my 50g version in HPGCC2. If any want the binary let me know and I'll post it. (When I have time I may finish my 41 version.)

This version will solve for x2 - Ny2 = 1 or x2 - Ny2 = -1.

To use, put N and 1 or 0 on the stack (1 if you want to solve for 1 and 0 for -1).

Returned to the stack in levels 2 and 1 will be x and y. An error is returned for no solution. NOTE: when solving for x2 - Ny2 = -1, N may not have a solution even if not a perfect square, e.g. N = 3.

Example output (results are returned instantly): 

(61,1)      1766319049       226153980
(94,1)         2143295          221064 
(97,1)        62809633         6377352
(61,0)           29718            3805
(94,0)                     No Solution
(97,0)            5604             569

(9781,1):

x = 4762537591409034590155570371480382426939162170819709
    1121919391568721296538714974921008596574575395059975
    2054760793982856538711730939866434465866978234993801 

y = 4815559876082440302661477925425109987613771229009146
    4260820131965621987686970309209803127165782081289861
    90989127348406759507489241673054751368237330579140
Some observations not mentioned above:
  1. x and y have opposite parity.
  2. x and y are co-prime.
C code: 
#include <hpgcc49.h>
#include <tommath.h>

int main(int argc, char **argv) {
    mp_int D, temp1, temp2, P2, P3, Q2, Q3, a1, a2, a3, p1, p2, p3, q1, q2, q3;
    int e, d, k = 0;
    char buf[10000];

    sys_slowOff();

    mp_init(&D); mp_init(&temp1); mp_init(&temp2);
    mp_init(&P2); mp_init(&P3); mp_init(&Q2); mp_init(&Q3);
    mp_init(&a1); mp_init(&a2); mp_init(&a3);
    mp_init(&p1); mp_init(&p2); mp_init(&p3);
    mp_init(&q1); mp_init(&q2); mp_init(&q3);

    e = sat_pop_real(); if(e != 0) e = 1;
    d = sat_pop_real();

    mp_set_int(&D,d);
    mp_sqrt(&D,&a1);                // a1 = sqrt(D);
    mp_copy(&a1,&p1);                // p1 = a1;
    mp_set_int(&q1,1);                // q1 = 1;
    mp_copy(&a1,&P2);                // P2 = a1;
    mp_sqr(&a1,&temp1);                // Q2 = D - a1*a1;
    mp_sub(&D,&temp1,&Q2);

    if(mp_iszero(&Q2)) {
        sprintf(buf,"No Solution for %d!\n",d);
        sat_stack_push_string(buf);
        sat_push_real(1);
        return(0);
    }

    mp_add(&a1,&P2,&temp1);            //a2 = (a1+P2)/Q2;
    mp_div(&temp1,&Q2,&a2,&temp2);
    mp_mul(&a1,&a2,&temp1);            //p2 = a1*a2 + 1;
    mp_set_int(&temp2,1);
    mp_add(&temp1,&temp2,&p2);
    mp_copy(&a2,&q2);                //q2 = a2;

    if(mp_cmp(&Q2,&temp2) == 0) {
        mp_toradix(&D, buf, 10);
        printf("%15s ",buf);
        if(!e) {
            mp_toradix(&p1, buf, 10);
            printf("%15s ",buf);
            sat_stack_push_string(buf);
            mp_toradix(&q1, buf, 10);
            printf("%15s ",buf);
            sat_stack_push_string(buf);
            sat_push_real(0);
        }
        else {
            mp_toradix(&p2, buf, 10);
            printf("%15s ",buf);
            sat_stack_push_string(buf);
            mp_toradix(&q2, buf, 10);
            printf("%15s ",buf);
            sat_stack_push_string(buf);
            sat_push_real(0);
        }
        return(0);
    }

    while(1) {
        k++;
        mp_mul(&a2,&Q2,&temp1);        //P3 = a2*Q2 - P2;
        mp_sub(&temp1,&P2,&P3);
        mp_sqr(&P3,&temp1);            //Q3 = (D-P3*P3)/Q2;
        mp_sub(&D,&temp1,&temp2);
        mp_div(&temp2,&Q2,&Q3,&temp1);

        mp_set_int(&temp2,1);
        if(mp_cmp(&Q3,&temp2) == 0) {
            if(e && k % 2 == 1)
                break;
            if(!e)
                if(k % 2 == 0)
                    break;
                else {
                    sprintf(buf,"No Solution for %d!\n",d);
                    sat_stack_push_string(buf);
                    sat_push_real(1);
                    return(0);
                }
        }

        mp_add(&a1,&P3,&temp1);        //a3 = (a1+P3)/Q3;
        mp_div(&temp1,&Q3,&a3,&temp2);
        mp_mul(&a3,&p2,&temp1);        //p3 = a3*p2 + p1;
        mp_add(&temp1,&p1,&p3);
        mp_mul(&a3,&q2,&temp1);        //q3 = a3*q2 + q1;
        mp_add(&temp1,&q1,&q3);
        mp_copy(&p2,&p1);            //p1 = p2;
        mp_copy(&p3,&p2);            //p2 = p3;
        mp_copy(&q2,&q1);            //q1 = q2;
        mp_copy(&q3,&q2);            //q2 = q3;
        mp_copy(&P3,&P2);            //P2 = P3;
        mp_copy(&Q3,&Q2);            //Q2 = Q3;
        mp_copy(&a3,&a2);            //a2 = a3;
    }

    mp_toradix(&p2, buf, 10);
    printf("%15s ",buf);
    sat_stack_push_string(buf);

    mp_toradix(&q2, buf, 10);
    printf("%15s ",buf);
    sat_stack_push_string(buf);
    sat_push_real(0);

    return(0);
}

Wrapper: 

%%HP: T(3)A(R)F(.);
\<< \-> d e
  \<< d \->NUM e \->NUM
    "EXTEND/PELL" 3 \->TAG EVAL
    IF THEN
      DOERR
    END
    OBJ\-> SWAP
    OBJ\-> SWAP
  \>>
\>>

Edited: 21 Jan 2009, 6:27 p.m.

            
Re: x^2 - N*y^2 = 1 (12C)
Message #18 Posted by Brent Hillebrenner on 21 Jan 2009, 8:49 p.m.,
in response to message #17 by Egan Ford

Hello -

I get the following in sage for N = 94:

(94, [2143295, 221064])

verified at the link in this thread

I'm curious if your routine finds the answer for N = 109 or N = 157? Mine fails miserably. It fails for 9781 too.

                  
Re: x^2 - N*y^2 = 1 (12C)
Message #19 Posted by Egan Ford on 22 Jan 2009, 12:18 a.m.,
in response to message #18 by Brent Hillebrenner

Quote:
I get the following in sage for N = 94:

(94, [2143295, 221064])

As do I if x2 - Ny2 = 1, but there is no solution for N = 94 if x2 - Ny2 = -1.
Quote:
I'm curious if your routine finds the answer for N = 109 or N = 157? Mine fails miserably. It fails for 9781 too.
I get for x2 - Ny2 = 1: 
 N         x                y                C          J
--- ---------------  --------------          -         -- 
109 158070671986249  15140424455100          1         29
157  46698728731849   3726964292220          1         33
C is the value if x and y are plugged into x2 - Ny2 (should be 1), and J is the number of iterations required. I suspect that your recursive approach may be running out of memory. Your recursive depth will be J. My program is iterative, it has to be to run in less than 400K of RAM.

BTW, I get for x2 - Ny2 = -1: 

 N         x                y                C          J
--- ---------------  --------------          -         --
109         8890182          851525         -1         14
157         4832118          385645         -1         16
                  
Re: x^2 - N*y^2 = 1 (12C)
Message #20 Posted by Egan Ford on 22 Jan 2009, 2:03 a.m.,
in response to message #18 by Brent Hillebrenner

Quote:
Mine fails miserably. It fails for 9781 too.
I just tried your program on my Sage server and got the following output: 
WARNING: Output truncated!  
full_output.txt

Traceback (click to the left for traceback)
...
RuntimeError: maximum recursion depth exceeded

WARNING: Output truncated!  
full_output.txt
I am unsure how to adjust this. Google should know. :-)
                        
Re: x^2 - N*y^2 = 1 (12C)
Message #21 Posted by Brent Hillebrenner on 22 Jan 2009, 7:17 a.m.,
in response to message #20 by Egan Ford

Well... this isn't a sage forum, although it wouldn't be a bad
idea to have a calculator that runs something similar. Egan, I
think you first mentioned it at this forum. I checked it out
and I like it.

As for my algorithm, I think it fails in calculating the
partial quotient(???) for numbers with larger solutions.
                              
Re: x^2 - N*y^2 = 1 (12C)
Message #22 Posted by Egan Ford on 22 Jan 2009, 12:10 p.m.,
in response to message #21 by Brent Hillebrenner

Quote:
As for my algorithm, I think it fails in calculating the partial quotient(???) for numbers with larger solutions.
It shouldn't. Integers in Sage are only limited by memory. You are just exceeding the maximum recursion depth.
                              
Re: x^2 - N*y^2 = 1 (12C)
Message #23 Posted by Egan Ford on 22 Jan 2009, 12:17 p.m.,
in response to message #21 by Brent Hillebrenner

Quote:
Well... this isn't a sage forum, although it wouldn't be a bad idea to have a calculator that runs something similar.
I think the 50g is very close. It has a powerful programming language (UserRPL), CAS, graphics, and can be extended with C.

Sage is based on Python with a bunch of open source extensions. I think for a hand held the 50g is good enough.

If you really want Sage to go, then setup your own Sage server in cyberspace and use your iPhone web browser. It works OK, but without Java you miss out on any interactive applications.

As for Python in your pocket (or Sage for that matter). I've done the former. I had a Python development environment on my Zaurus. It was huge and slow. Now a Lua interface to Sage C-based extensions--that would be great.

There is already talk about multicore iPhones and PDAs, just wait and you'll be able to run Sage on it as is.

            
Re: x^2 - N*y^2 = 1 (12C)
Message #24 Posted by Gerson W. Barbosa on 23 Jan 2009, 5:20 a.m.,
in response to message #17 by Egan Ford

Hello Egan,

You always get more than you ask for here :-) Thanks everybody who participated.

As I didn't add comments to my HP-12C version, here is the equivalent TurboBCD version. Function Sqrt(x) has been included because TurboBCD lacks this one and the transcendental functions. The output shows the convergents to rational approximations of Sqrt(N) until the first solution is found.

Gerson. 


---------------------------

Program Pell;

var b, c, d, k, n, n0, r, s, t, x: Real;

function Sqrt(x: Real): real;

var s, t: Real;

begin
  if x<>0 then
    begin
      s:=x/2;
      repeat
        t:=s;
        s:=(s+x/s)/2
      until s=t;
      Sqrt:=s
    end
    else
      Sqrt:=0
end;

begin
  ClrScr;
  ReadLn(k);
  ClrScr;
  r:=Sqrt(k);
  n0:=1;
  d:=1;
  n:=Int(r);
  b:=Frac(r);
  c:=Int(1/b);
  repeat
    t:=n;
    n:=c*n+n0;
    d:=Int(n/r+0.5);
    b:=Frac(1/b);
    c:=Int(1/b);
    n0:=t;
    WriteLn(n:10:0,'  /',d:9:0,'   = ',n/d:19:16)
  until n*n-k*d*d=1;
  Writeln;
  Writeln(' ':14,'Sqrt(',k:3:0,' ) = ',r:19:16)
end.

---------------------------

        10  /        1   = 10.0000000000000000
        59  /        6   =  9.8333333333333333
        69  /        7   =  9.8571428571428571
       128  /       13   =  9.8461538461538462
       197  /       20   =  9.8500000000000000
       325  /       33   =  9.8484848484848485
       522  /       53   =  9.8490566037735849
       847  /       86   =  9.8488372093023256
      4757  /      483   =  9.8488612836438923
      5604  /      569   =  9.8488576449912127
    105629  /    10725   =  9.8488578088578089
    111233  /    11294   =  9.8488578006020896
    661794  /    67195   =  9.8488578019197857
    773027  /    78489   =  9.8488578017301788
   1434821  /   145684   =  9.8488578018176327
   2207848  /   224173   =  9.8488578017870127
   3642669  /   369857   =  9.8488578017990737
   5850517  /   594030   =  9.8488578017945222
   9493186  /   963887   =  9.8488578017962687
  53316447  /  5413465   =  9.8488578017960770
  62809633  /  6377352   =  9.8488578017961060

              Sqrt( 97 ) =  9.8488578017961047

---------------------------
      
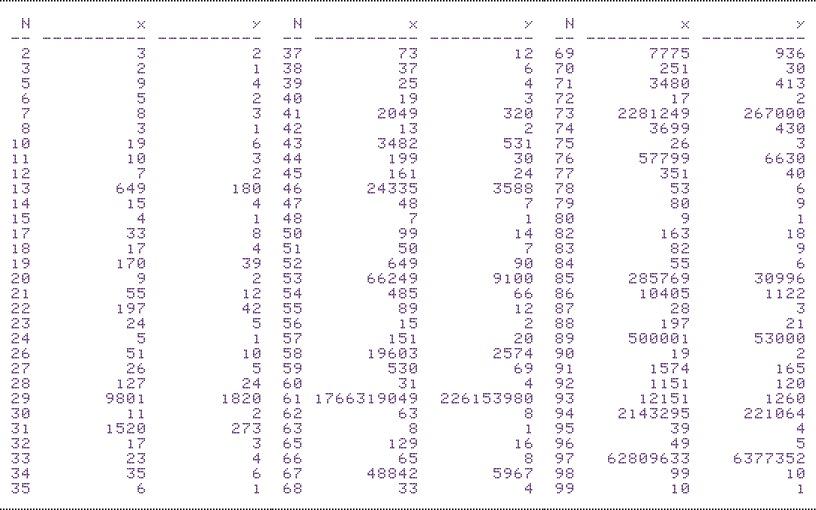
Re: x^2 - N*y^2 = +/- 1 (41CX)
Message #25 Posted by Egan Ford on 22 Jan 2009, 12:07 p.m.,
in response to message #1 by Gerson W. Barbosa

Here is my 41CX version. It is not very optimized. Like my 50g solution it will solve for x2 - Ny2 = 1 or x2 - Ny2 = -1.

To use, put N and 1 or 0 on the stack (1 if you want to solve for 1 and 0 for -1).

Returned to the stack will be x and y. An error is returned for no solution. NOTE: when solving for x2 - Ny2 = -1, N may not have a solution even if not a perfect square, e.g. N = 3.

x2 - Ny2 = 1 table created with 41CX PELL (N = 61 took 56 seconds):

x2 - Ny2 = -1 table created with 41CX PELL (N = 61 took 28 seconds):

Source, RAW, and Barcode: http://www.hpmuseum.org/guest/eganford/pell.zip.

i41CX+ users can always get my programs on-line here: http://sense.net/~egan/41cx.

Source: 

 01 LBL "PELL"           33 RCL 12               65 X#Y?                 97 RCL 08              
 02 STO 15               34 1                    66 GTO 05               98 *                   
 03 X<>Y                 35 X#Y?                 67 RCL 15               99 RCL 07              
 04 STO 00               36 GTO 02               68 X=0?                100 +                   
 05 SQRT                 37 RCL 15               69 GTO 06              101 STO 09              
 06 INT                  38 X#0?                 70 RCL 14              102 RCL 05              
 07 STO 01               39 GTO 04               71 2                   103 STO 04              
 08 STO 04               40 RCL 07               72 MOD                 104 RCL 06              
 09 STO 10               41 RCL 04               73 X=Y?                105 STO 05              
 10 1                    42 RTN                  74 GTO 04              106 RCL 08              
 11 STO 07               43 LBL 02               75 GTO 05              107 STO 07              
 12 RCL 00               44 0                    76 LBL 06              108 RCL 09              
 13 RCL 01               45 STO 14               77 RCL 14              109 STO 08              
 14 RCL 01               46 LBL 03               78 2                   110 RCL 11              
 15 *                    47 1                    79 MOD                 111 STO 10              
 16 -                    48 ST+ 14               80 X=0?                112 RCL 13              
 17 STO 12               49 RCL 02               81 GTO 04              113 STO 12              
 18 X=0?                 50 RCL 12               82 GTO 07              114 RCL 03              
 19 GTO 07               51 *                    83 LBL 05              115 STO 02              
 20 RCL 01               52 RCL 10               84 RCL 01              116 GTO 03              
 21 RCL 10               53 -                    85 RCL 11              117 LBL 04              
 22 +                    54 STO 11               86 +                   118 RCL 08              
 23 RCL 12               55 RCL 11               87 RCL 13              119 RCL 05              
 24 /                    56 *                    88 /                   120 RTN                 
 25 INT                  57 CHS                  89 INT                 121 LBL 07              
 26 STO 02               58 RCL 00               90 STO 03              122 -1                  
 27 STO 08               59 +                    91 RCL 05              123 CLA                 
 28 RCL 01               60 RCL 12               92 *                   124 >"NO SOLUTION"      
 29 *                    61 /                    93 RCL 04              125 AVIEW               
 30 1                    62 INT                  94 +                   126 RTN                 
 31 +                    63 STO 13               95 STO 06              127 END                 
 32 STO 05               64 1                    96 RCL 03
            
Re: x^2 - N*y^2 = +/- 1 (41CX)
Message #26 Posted by MikeO on 22 Jan 2009, 12:24 p.m.,
in response to message #25 by Egan Ford

Hi Egan, Thorough work as always!

What tool chain do you use to put 'C' programs the HP50G?

Thanks, Mike

                  
Re: x^2 - N*y^2 = +/- 1 (41CX)
Message #27 Posted by Egan Ford on 22 Jan 2009, 12:50 p.m.,
in response to message #26 by MikeO

Quote:
What tool chain do you use to put 'C' programs the HP50G?
HPGCC 2:

Windows/Linux: http://hpgcc.org

Mac: http://www.hydrix.com/Download/Hp/hpgcc/

Win/Lin/Mac Tutorial + simulator (HPAPINE) + tool chains: http://sense.net/~egan/hpgcc/. <- Start Here.

HPGCC 3:

HPGCC 3 has not been released, this is the only documentation that I have created: http://sense.net/~egan/hpgcc3/qsosx.html.

The HPGCC 3 beta supports Win/Lin/Mac. The emulator is for Lin/Mac only. The HPAPINE simulator used with HPGCC2 does not work with HPGCC3. The http://x49gp.svn.sourceforge.net/viewvc/x49gp/README.QUICKSTART emulator can be used for HPGCC2 and 3, but for Mac/Lin only.

Edited: 22 Jan 2009, 12:52 p.m.

                        
Re: x^2 - N*y^2 = 1 implies sqrt(N) irrational
Message #28 Posted by mjcohen on 23 Jan 2009, 8:21 p.m.,
in response to message #27 by Egan Ford

An interesting note: If there is a positive integral solution to x^2 - n*y^2 = 1 for a positive integer n then sqrt(n) is irrational.

Proof (outline):

1. Show if there is one solution then there are arbitrarily large solutions. Proof: Show that (x^2-ny^2)(u^2-nv^2) = a^2-nb^2 where a and b are functions of x, y, u, and y.

2. If n = (r/s)^2 and x^2 - n*y^2 = 1 then we can get an upper bound on y as a function of s. Proof: Factor (x/y)^2 - (r/s)^2.

Contradiction!

This proof is interesting because it does not use any divisibility properties - only that two distinct integers are at least 1 apart.

Martin Cohen

      
Re: x^2 - N*y^2 = 1 (12C)
Message #29 Posted by Patrice on 24 Jan 2009, 4:23 p.m.,
in response to message #1 by Gerson W. Barbosa

Hi all,

As anyone tried to transform the formula as an equality of products?

x^2 - N * y^2 = 1

x^2 - 1 = N * y^2

(x-1) * (x+1) = N * y^2

Is it useful? (knowing that x, N and y are integers)

Patrice

            
Re: x^2 - N*y^2 = 1 (12C)
Message #30 Posted by Palmer O. Hanson, Jr. on 24 Jan 2009, 9:41 p.m.,
in response to message #29 by Patrice

Patrice:

You wrote:

Quote:
Has anyone tried to transform the formula as an equality of products?

x^2 - N * y^2 = 1

x^2 - 1 = N * y^2

(x-1) * (x+1) = N * y^2

Is it useful? (knowing that x, N and y are integers)

I looked at this with the N moved to the other side so that the left side was (x-1)(x+1)/N. I concluded that when N is even then (x-1)(x+1) will be odd and the division by an even N will yield a left side which is not an integer. Thus, when N is even as with 92, then x must be odd. Furthermore, when N is 92 then either (x-1) or (x+1) musr be divisible by 23 or the left side will not be an integer. I haven't been able to push anything through which would increase the speed of the solution.

Palmer

                  
Re: x^2 - N*y^2 = 1 (12C)
Message #31 Posted by Egan Ford on 25 Jan 2009, 11:45 a.m.,
in response to message #30 by Palmer O. Hanson, Jr.

Quote:
Thus, when N is even as with 92, then x must be odd. Furthermore, when N is 92 then either (x-1) or (x+1) must be divisible by 23 or the left side will not be an integer. I haven't been able to push anything through which would increase the speed of the solution.
x2 - 92y2 = 1 can be rewritten as x2 - 23(2Y)2 = 1. That would explain your 23 and why y would have to be even and therefore x odd.
            
Re: x^2 - N*y^2 = 1 (12C)
Message #32 Posted by Gerson W. Barbosa on 27 Jan 2009, 10:27 a.m.,
in response to message #29 by Patrice

Quote:
(x-1) * (x+1) = N * y^2

Is it useful? (knowing that x, N and y are integers)

I had tried y = (x-1)/N * (x+1)/y but I got rounding errors. The program would not loop for ever in case of large x or y but occasionally the answers would be wrong. For instance, on the HP-12C: 


   N         x         y
--------------------------
  61      469849     60158    should be 1766319049 and 226153980
  73     4854814    568213    should be    2281249 and    267000 
  85      285769     30996    ok
  89      216991     23001    should be     500001 and     53000 

Likewise, on TurboBCD:

   N         x                 y
------------------------------------
  61    1766319049         226153980  ok
1234    5955464517         169534489  should be 586327869067265 and 16691023073856 

----------

Program Pell;
var b, c, d, k, n, n0, r, s, t, x: Real;
function Sqrt(x: Real): real;
var s, t: Real;
begin
  if x<>0 then
    begin
      s:=x/2;
      repeat
        t:=s;
        s:=(s+x/s)/2
      until s=t;
      Sqrt:=s
    end
    else
      Sqrt:=0
end;
begin
  ClrScr;
  ReadLn(k);
  r:=Sqrt(k);
  n0:=1;
  d:=1;
  n:=Int(r);
  b:=Frac(r);
  c:=Int(1/b);
  repeat
    t:=n;
    n:=c*n+n0;
    d:=Int(n/r+0.5);
    b:=Frac(1/b);
    c:=Int(1/b);
    n0:=t
  until d=(n+1)/k*(n-1)/d;
  WriteLn(n:20:0,d:18:0)
end.

Gerson.

[ Return to Index | Top of Index ]

Go back to the main exhibit hall