By Erik Ehrling (Sweden). Any comments or suggestions are very welcome!
This program is supplied without representation or warranty of any kind. Erik Ehrling and The Museum of HP Calculators therefore assume no responsibility and shall have no liability, consequential or otherwise, of any kind arising from the use of this program material or any part thereof.
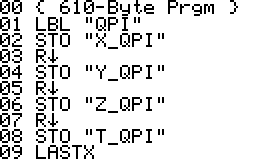
This is a version of QPI for the HP42S, based on the program with the same name for the HP48 by Mika Heiskanen and André Schoorl. It finds rational approximations to decimal numbers on the forms nom/den, √(nom/den), nom/den×pi, ln(nom/den), e(nom/den) - choosing the form that seems most suitable.
Usage:
Using QPI is simple, just enter a decimal number in the range -9.99999999E9 .. 9.99999999E9 and run QPI. The rational approximation takes a few seconds and the result will be displayed in the upper area of the display. The result is also stored in the alpha register. Note that the stack, all numbered registers and user flags are left unaltered. It is therefore possible to run QPI in the middle of a calculation and then continue after it has run.
Examples:
Technical notes:
Binary files for emulators:
State-file for Emu42: qpi.e42 Raw binary: qpi.raw Binary for HP-42X: qpi.42x

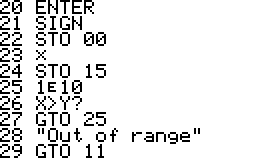
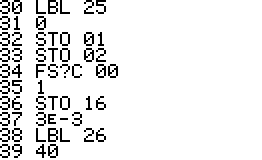
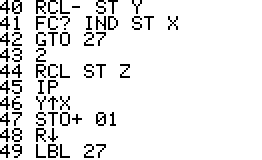
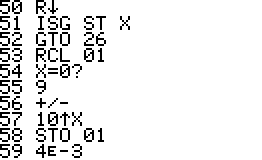
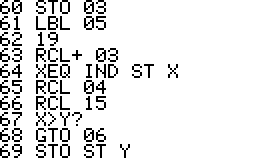

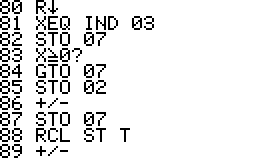
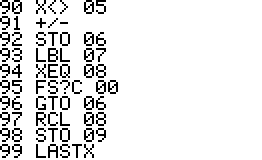

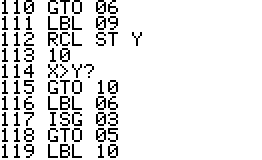
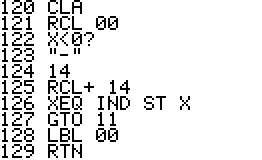

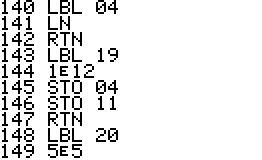
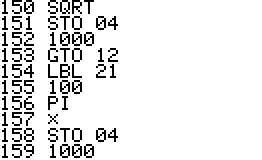
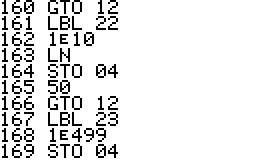



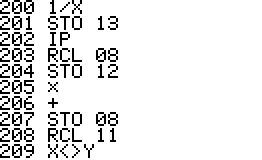
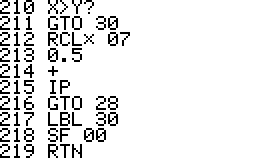
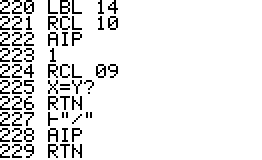
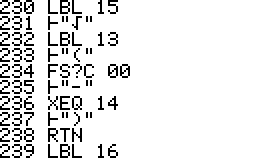



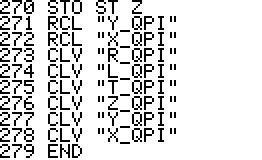
![]() Go back to the general software library
Go back to the general software library
![]() Go back to the main exhibit hall
Go back to the main exhibit hall