This program is Copyright © 1976 by Hewlett-Packard and is used here by permission. This program was originally published in the HP-67 Standard Pac.
This program is supplied without representation or warranty of any kind. Hewlett-Packard Company and The Museum of HP Calculators therefore assume no responsibility and shall have no liability, consequential or otherwise, of any kind arising from the use of this program material or any part thereof.
| Curve Fitting | |||||
| Shift | P? | LIN? | EXP? | LOG? | PWR? |
| Label | xi↑yi(+) | xi↑yi(-) | →r2,a,b | y→x̂ | x→ŷ |
| Key | A | B | C | D | E |
This program can be used to fit data to:
The type of curve fit must be determined before data input begins. To select linear regression, you would press the f B keys. To select exponential curve fit, press f C. To select logarithmic curve fit, press f D - To select power curve fit, press f E. Do not attempt to change from one type of fit to another after data input has begun because the summation registers are cleared when the type of curve fit is selected. Restarting can be accomplished by repeating the curve fit selection process.
Data pairs (xi and yi) are input by keying in xi, pressing ENTER↑ keying in yi and pressing the A key. Any number of data pairs may be input. If, after pressing the A key, you discover a data pair was incorrect, wait until execution stops, press h R↓ then the B key. This will eliminate the errant data pair. If you wish to eliminate any data pair previously input, key it in (x ENTER↑ y) and press B.
After all data pairs have been input, press C. This initiates calculation and output of the coefficient of determination r2, and the regression coefficients a and b. The coefficient of determination indicates the quality of fit achieved by the regression. Values of r2 close to 1.00 indicate a better fit than values close to zero. The regression coefficients a and b define the curve generated, according to the equations at the beginning of this discussion.
After the regression coefficients have been calculated, projections may be made based on the curve fit. Key in a known x value, press E and see an estimated y value, ŷ, or key in a known y value, press D and see an estimated x value, x̂.
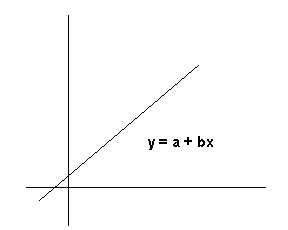
Σxiyi - (ΣxiΣyi)/n
b = ---------------------------
Σxi2 - (Σxi)2/n
a = [Σyi/n - bΣxi/n]
[Σxiyi - (Σxi*Σyi)/n]2
r2 = --------------------------------------------------
[Σxi2 - (Σxi)2/n][Σyi2 - (Σyi)2/n]
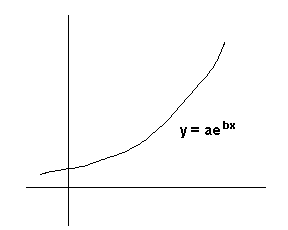
Σxi ln yi - (ΣxiΣ ln yi)/n
b = ------------------------------------
Σxi2 - (Σxi)2/n
a = exp[(Σ ln yi)/n - b*(Σxi)/n]
[Σxi ln yi - (ΣxiΣ ln yi)/n]2
r2 = --------------------------------------------------
[Σxi2 - (Σxi)2/n][Σ(ln yi)2 - (Σ ln yi)2/n]
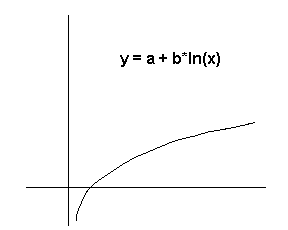
Σyi*ln xi - (Σ ln xiΣyi)/n
b = -----------------------------
Σ(ln xi)2 - (Σ ln xi)2/n
a = (Σyi - bΣ ln xi)/n
[Σyi ln xi - Σ ln xiΣyi/n]2
r2 = --------------------------------------------------
[Σ(ln xi)2 - (Σ ln xi)2/n][Σyi2-(Σyi)2/n]
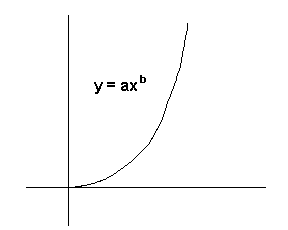
Σ(ln xi)(ln yi) - (Σ ln xi)(Σ ln yi)/n
b = -------------------------------------
Σ(ln xi)2 - (Σ ln xi)2/n
a = exp[(Σ ln yi)/n - b(Σ ln xi)/n]
[Σ(ln xi)(ln yi) - (Σ ln xi)(Σ ln yi)/n]2
r2 = -----------------------------------------------------
[Σ(ln xi)2 - (Σ ln xi)2/n][Σ(ln yi)2 - (Σ ln yi)2/n]
Negative and zero values of xi will cause a machine error for logarithmic curve fits. Negative and zero values of yi will cause a machine error for exponential curve fits. For power curve fits both xi, and yi must be positive, non-zero values.
Registers R0-R9 are available for user storage.
It is not necessary to key in the x value if it corresponds to the counter returned to the display (see example 1).
As the differences between x and/or y values become small, the accuracy of the regression coefficients will decrease.
| Step | Instructions | Input Data/Units | Keys | Output Data/Units |
| 1 | Load side 1 and side 2. | |||
| 2 | Optional: Select pause input mode. | f A | 1.00 or 0.00 | |
| 3 | Select type of regression: | |||
| for linear fit | f B | 1.00 | ||
| for exponential fit | f C | 1.00 | ||
| for logarithmic fit | f D | 1.00 | ||
| for power fit | f E | 1.00 | ||
| 4 | Input x value*. | xi | ENTER↑ | xi |
| 5 | Input y value. | yi | A | i+1 |
| 6 | Repeat steps 4 and 5 for all data pairs**. | |||
| 7 | Compute and output coefficient of determination r2 and a and b. | C | r2, a, b | |
| 8 | Optional: Make projections based on a known y value. | y | D | est. x |
| 9 | Optional: Make projections based on a known x value. | x | E | est. y |
| 10 | For a new case go to step 3. | |||
| *Note that this step may be skipped if the x value equals the displayed counter (i + 1). | ||||
| **The last set of data pairs may be deleted by pressing h R↓ then B. Any set of data pairs may be deleted by entering them as in steps 4 and 5 and pressing B. |
Below is the sales data for the first 6 months of a product's life. According to a linear projection, what should the sales be after 12 months? When would sales reach the 150 unit per month mark assuming constant linear growth.
Month 1 2 3 4 5 6 Sales 15 37 52 59 83 92
Keystrokes Outputs
f B 1.00
15 A 37 A 52 A 59 A 83 A 92 A 7.00
C 0.98 *** (r2)
3.33 *** (a)
15.14 *** (b)
12 E 185.05 units
150 D 9.69 months
The velocity of a particle experiencing constant acceleration is expressed by v = v0 + at where v is the velocity, v0 is the initial velocity, a is the acceleration and t is the time since v = v0.
The following data was experimentally obtained for a particle:
t(sec) V(m/sec)
5 140
6 149
7 159
9 175
What was the velocity at t = 0? What will the velocity be when t = 20? Note that the equation for velocity v = v0 + at is the equation of a straight line and is analogous to y = a + bx. Therefore use linear regression with v substituted for y, v0 for a, a (acceleration) for b and t for x.
Keystrokes Outputs
f B 1.00
5 ENTER↑ 140 A 6 ENTER↑ 149 A
7 ENTER↑ 159 A 4.00
9 ENTER↑ 175 A C 1.00 *** (r2)
96.54 *** (a, v0)
8.77 *** (b, acceleration)
20 E 271.97 *** (m/sec)
Many compression processes can be correlated using the power curve p = av-b where b is the polytropic constant of the process.
Pressure-volume data for a compression process is shown below. Run a power curve fit to determine the polytropic constant, -b. What is the pressure when v is 15?
v p 10 210 30 40 50 12 70 9 90 6.8
Keystrokes Outputs
f E 1.00
10 ENTER↑ 210 A 30 ENTER↑ 40 A
50 ENTER↑ 12 A 4.00
70 ENTER↑ 9 A 90 ENTER↑ 6.8 A
C 0.99 *** (r2)
8599.81 *** (a)
-1.62 *** (-b)
15 E 108.35
LINE KEYS 001 *LBL a Toggle print/pause mode flag. 002 0 003 F2? 004 RTN 005 1 006 SF 2 007 RTN 008 *LBL b Clear flags and registers for linear 009 CF 0 regression. 010 CF 1 011 P⇔S 012 CL REG 013 P⇔S 014 1 015 RTN 016 *LBL c Call LBL b, then set exponential flag. 017 GSB b 018 SF 1 019 RTN 020 *LBL d Call LBL b, then set the logarithmic flag. 021 GSB b 022 SF 0 023 RTN 024 *LBL e Call LBL d, then set the power curve flag. 025 GSB d 026 SF 1 027 RTN 028 *LBL A Clear Σ- flag. 029 CF 3 030 *LBL 8 031 F2? Print if flag 2 is set. 032 GSB 9 033 STO D 034 F1? ln y if flag 1 is set. 035 LN 036 X⇔Y ln x if flag 0 is set. 037 STO C 038 F0? 039 LN 040 F3? If flag 3, then Σ-. 041 GTO 0 042 Σ+ Compute sums. 043 *LBL 7 Calculate i + 1. 044 ENTER↑ 045 1 046 + 047 RCL C Set inputs in stack positioned for possible 048 X⇔Y deletion. 049 RCL D 050 X⇔Y 051 RTN 052 *LBL 0 Subtract from sums. 053 Σ- 054 GTO 7 055 *LBL 9 Print inputs and reset print flag. 056 PRT SPC 057 X⇔Y 058 PRTX 059 X⇔Y 060 PRTX 061 SF 2 062 RTN 063 *LBL B 064 SF 3 Set Σ- flag. 065 F2? Print delete indicator if flag is set. 066 GSB 3 067 GTO 8 Delete inputs. 068 *LBL C Switch to secondary registers. 069 P⇔S 070 PRT SPC Compute b. 071 RCL 8 072 RCL 4 073 RCL 6 074 × 075 RCL 9 076 ÷ 077 - 078 ENTER↑ 079 ENTER↑ 080 RCL 4 081 x2 082 RCL 9 083 ÷ 084 RCL 5 085 X⇔Y 086 - 087 ÷ 088 STO B 089 × Compute r2. 090 RCL 6 091 x2 092 RCL 9 093 ÷ 094 CHS 095 RCL 7 096 + 097 ÷ 098 PRTX 099 RCL 6 Compute a. 100 RCL 4 101 RCL B 102 × 103 - 104 RCL 9 105 ÷ 106 F1? 107 eX 108 STO A 109 PRTX Output a and b. 110 RCL B 111 PRTX 112 P⇔S Switch registers. 113 RTN 114 *LBL E Position coefficients in stack for use by 115 STO E projection routines. 116 RCL A 117 RCL B 118 RCL E 119 F1? If flag 1 is set, power or exponential 120 GTO 1 projection. 121 F0? 122 LN Logarithmic? 123 × 124 + Linear or logarithmic projection. 125 F2? 126 GTO 9 Print? 127 RTN Stop 128 *LBL 1 129 F0? If flag 0 is set, do power fit. 130 GTO 2 131 × Do exponential projection. 132 eX 133 × 134 F2? Print? 135 GTO 9 136 RTN Stop 137 *LBL 2 138 X⇔Y 139 Yx Do power projection. 140 × 141 F2? Print? 142 GTO 9 143 RTN Stop 144 *LBL 3 145 PRT SPC Print -1 indicator. 146 1 147 CHS 148 PRTX 149 SF 2 150 R↓ 151 RTN 152 *LBL D Position coefficients in stack for use by 153 STO E projection routine. 154 RCL B 155 1/X 156 RCL A 157 RCL E 158 X⇔Y 159 F1? 160 GTO 1 Power or exp? 161 - 162 × Linear and log projection. 163 F0? 164 ex Logarithmic. 165 F2? Print? 166 GTO 9 167 RTN Stop 168 *LBL 1 169 ÷ Calculate exp calc. 170 F0? For power, GTO 1 171 GTO 1 172 LN Exponential projection. 173 × 174 F2? 175 GTO 9 Print? 176 RTN Stop 177 *LBL 1 178 X⇔Y Power projection. 179 YX 180 F2? Print? 181 GTO 9 182 RTN Stop 183 R/S
S0 0 S1 0 S2 0 S3 0 S4 Σx S5 Σx2 S6 Σy S7 Σy2 S8 Σxy S9 n A a B b C xi D yi E x,y I 0
![]() Go back to the software library
Go back to the software library
![]() Go back to the main exhibit hall
Go back to the main exhibit hall