This program is Copyright © 1976 by Hewlett-Packard and is used here by permission. This program was originally published in the HP-67 Standard Pac.
This program is supplied without representation or warranty of any kind. Hewlett-Packard Company and The Museum of HP Calculators therefore assume no responsibility and shall have no liability, consequential or otherwise, of any kind arising from the use of this program material or any part thereof.
| Calculus And Roots Of f(X) | |||||
| Shift | (%Δ) | Pause? | |||
| Label | 1,2,3,4,5? | x→f'(x) | x→f(x) | n↑a↑b→∫a..b | x0→root |
| Key | A | B | C | D | E |
This program incorporates four routines for numerical analysis of user specified functions. Suppose the figure below represents a known function of x called f(x).
If the formula for f(x) can be keyed into program memory in less than 112 steps (including LBL and RTN), this program can be used to find the value of f(x) at any point x, the derivative of f(x) at any point x, the integral of f(x) over a specified interval and the real roots of f(x). There may be up to five different f(x) functions in program memory at one time. They must be labeled from 1 to 5. The function to be evaluated is selected by keying in 1, 2, 3, 4 or 5 and pressing A.
Only side 1 of Calculus and Roots of f(x) is used for the program. In the listing below, side two (steps 112-223) lists functions used in the examples. You may wish to add functions you use frequently to side 2 of this card or record them on additional magnetic cards. Once recorded, the functions can be linked to Calculus and Routs of f(x) by the following sequence of operations:
Once a function is defined and selected, keying in a value of x and pressing the C key will result in the evaluation of f(x) (see below).
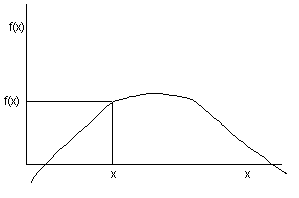
Similarly, the value of the slope of f(x) at a particular point x can be calculated by keying in x and pressing the B key (see figure below). The slope of f(x) is determined using an approximation to the differential:
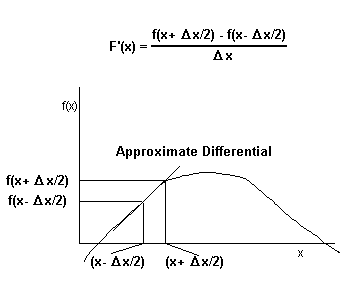
The value of Δx used to approximate the differential is assumed to be 0.01% of x (10-4 * x) unless a %Δ is specified by the user. That is:
Δx = %Δ/100 * x
In the special case where x = 0, Δx is set equal to %Δ.
For most applications, the assumed value of 0.01% should be adequate. In some cases more accurate results can be obtained using a smaller value of %Δ. However, care must be taken to assure that the calculator can accurately resolve the difference between f(x- Δx/2) and f(x + Δx/2).
The D key may be used to approximate the integral or area under a curve.

You specify the end points of the interval (a and b) and the number of rectangles (n) the interval should be broken into (see figure above). The calculator computes the sum of the areas of the rectangles. The more rectangles used the closer this value is to the actual area under the curve. However, more rectangles mean more computation time. Experience with a particular function should lead to a balance between accuracy and execution time.
Root finders are used to solve equations which are difficult or impossible to solve explicitly. An example of such an equation is
f(x) = ln x + 3x - 10.8074 = 0
which is solved in example 4.
The root finder incorporated in this program uses a secant method of approximation. You must supply the routine with an initial guess of the root. Based on this guess, it will attempt to make better and better approximations of the root by the following formula:
xi+1 = xi - f(xi)[(xi - xi-1)/(f(xi) - f(xi-1))]
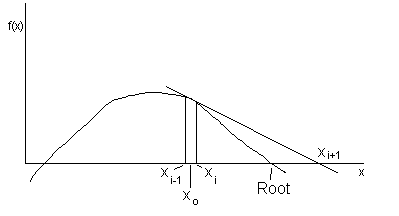
The display is automatically set to fix mode during the root finder portion of the program. When the last approximation is accurate to the number of places specified by the display setting of the calculator, the routine halts and displays the root.
Since the root finder starts its search based on your guess, care should be exercised in guess selection. A bad guess will cause long execution times and could result in a machine status error halt (overflow, division by zero, log of a negative number, etc.). If this happens, simply try another guess. Practice will make the pitfalls more obvious and easier to avoid.
A special feature of the iterative routine is the pause function. This feature allows the program to pause at one point in each iteration to display the current approximation of the root. The pause option may be turned off and on by pressing f E. The pause allows you to watch the routine converge (or diverge) without interrupting the program. This can be a helpful tool when the iterative routine fails to converge. By watching each successive approximation of the root, the reasons for failure of convergence can usually be determined.
The value of x is stored in R0 by the program. It is also in the X register when control transfers to the function subroutine.
Registers R1-R8, and RS0-RS9 are available for use in f(x) or for other user storage.
User-specified functions may use one level of subroutine nesting.
The secant method does not guarantee convergence to a root. If it fails, use Solution to f(x) on an interval.
Given one guess, the root finder will find, at most, one root of an equation. Other real roots, if they exist, may be found by modifying the initial guess.
In order to compute f'(x), the function f(x) must be continuous on the interval (x + Δx/2, x - Δx/2).
| Step | Instructions | Input Data/Units | Keys | Output Data/Units |
| 1 | Load side 1. | |||
| 2 | Load subroutine(s) (either key them in or link from program step 112). | |||
| 3 | Select function label number. | i (1-5) | A | i |
| 4 | Store any constants necessary to subroutine(s) loaded in step 2. | |||
| 5 | For differentiation, go to step 6. For evaluation of a function, go to step 9. For integration of a function, go to step 11. To find a root, go to step 15. | |||
| 6 | Optional: Key in percent delta. | %Δ | f A | %Δ |
| 7 | Key in x and calculate derivative at x. | x | B | fi'(x) |
| 8 | For new x, go to step 7. For a new case, go to step 2, 3, 4, 5 or 6. | |||
| 9 | Key in x and evaluate function. | x | C | fi(x) |
| 10 | For new x, go to step 9. For a new case, go to step 2, 3, 4, or 5. | |||
| 11 | Input the number of intervals. | n | ENTER↑ | n |
| 12 | Input the lower limit. | a | ENTER↑ | a |
| 13 | Input the upper limit and calculate the integral. | b | D | ∫fi(x)dx |
| 14 | For new limits or interval, go to step 11. For a new case, go to step 2, 3, 4 or 5. | |||
| 15 | Optional: Key in percent delta. | %Δ | f A | %Δ |
| 16 | Optional: Toggle pause mode. | f E | 1.00 or 0.00 | |
| 17 | Key in guess and calculate root. | GUESS | E | x |
| 18 | For a new guess go to step 17. For a new case go to step 2, 3, 4 or 5. |
Numerical integration provides the only solution to the complete elliptic integral of the first kind:
u = ∫(0..π/2)dθ/√(1-K2sinθ2)
Find the value of u for limits of integration of 0.0 to π/2 Let K be 0.5 and store it in register 1 for access by the program. Use 3 and then 10 for the number of intervals. The formula for the integral is listed under label three of the listing below. If either example 2 or example 3 has just been run, skip the first three lines under keystrokes.
Keystrokes Outputs
Load side 1 only
GTO . 112 MERGE
Load side 2 (If you've entered
the examples)
Select label 3 3.00
3 A
0.50 STO 1 0.50
Integrate using 3 intervals
DSP 9 3 ENTER 0 ENTER↑
h π 2 ÷ D 1.685750251
Integrate using 10 intervals
10 ENTER 0 ENTER↑
h π 2 ÷ D 1.685750355
In the design of gear teeth, it is frequently necessary to calculate x for a given value of the involute:
INV(x) = tan x - x
or restated
f(x) = tan x - x - INV(x) = 0
If the involute of x is 0.0049819, what is x? This problem requires an iterative solution since the equation cannot be explicitly solved for x. Use 0.21 radians as your initial guess. The equation for f(x) is listed under label 2 in the program listing. Use the pause feature to watch the routine converge. Skip the first three lines under keystrokes if Example 1 or 3 has been run. Store the involute (.0049819) in R2 for access by the function.
Keystrokes Outputs
Load side 1 only
GTO . 112 MERGE
Load side 2
Select label 2
2A 2.00
Set pause
DSP 2 f E 1.00
.0049819 STO 2 .21 E "0.25"
"0.24"
"0.24"
0.24 (rad)
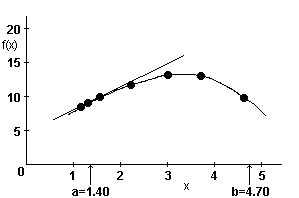
In many instances, a function is represented graphically. This program can be of use in integration and, in some cases, differentiation of such graphs. Label 1 in the listing below is designed for this purpose. It returns x values to the display. You must find f(x) from the graph, key it in and press R/S. For the function below find the integral from a to b using 5 intervals. Then find the derivative at a, using 10% for %Δ. After the problem is complete, return %Δ to 0.01%. If either Example 1 or Example 2 was run previously, skip the first three lines under keystrokes.
Keystrokes Outputs Load side 1 only GTO . 112 g MERGE Load side 2 Select Label 1 1 A 1.00 Key in integration limits and return first x value 5 ENTER↑ 1.40 ENTER↑ 4.70 D 1.73 (x) From the graph, f(x) at x = 1.73 equals 14.2. Key 14.2 in and press R/S. The next value of x will be displayed. 14.2 R/S 2.39 f(2.39) = 16 16 R/S 3.05 f(3.05) = 17 17 R/S 3.71 f(3.71) = 16.9 16.9 R/S 4.37 f(4.37) = 15.3 15.3 R/S 52.40 (answer) To find the derivative at point a 10 f A 1.40 B 1.33 (x - Δx/2) f(1.33) = 12.7 12.7 R/S 1.47 (x + Δx/2) f(1.47) = 13.3 13.3 R/S 4.29 (slope) Return %Δto 0.01% .01 f A 0.01
Find the root of ln x + 3x - 10.8074 = 0. Determine the slope at the root. This equation is not listed below. It should be keyed into program memory starting at step 112. Use R1 to store the 3 and R2 to store 10.8074.
Keystrokes Outputs
Load side 1 only
GTO . 112
Switch to W/PRGM 112 35 22
f LBL 1 31 25 01
f LN 114 31 52 (ln x)
RCL 1 115 34 01
RCL 0 116 34 00
x 117 71
+ 118 61 (ln x + 3x)
RCL 2 119 34 02
- 120 51 (ln x + 3x -
10.8074)
h RTN 121 35 22
Switch to Run
Select LBL 1
1 A 1.00
3 STO 1 3.00
10.8074 STO 2 10.81
Make a guess of 5.0
5 E 3.21 (ROOT)
Find the derivative
B 3.31 f'(3.21)
LINE KEYS 001 *LBL A Store function number. 002 STO I 003 RTN 004 *LBL e Pause toggle. 005 F0? 006 GTO 0 007 SF 0 008 1 009 RTN 010 *LBL 0 011 0 012 CF 0 013 RTN 014 *LBL a Store %Δ and set flag. 015 SF 1 016 STO E 017 RTN 018 *LBL B Choose default %Δ or use 0.01%? 019 EEX 020 CHS 021 2 022 RCL E 023 F1? 024 X⇔Y 025 R↓ 026 % If x=0 use %Δ rather than % of x as Δx. 027 X=0? 028 LST X 029 STO C 030 2 031 ÷ f(x-Δx/2) 032 - 033 STO A 034 STO 0 035 GSB (i) 036 STO D 037 RCL A [f(x+Δx/2)-f(x-Δ/2)]/Δx 038 RCL C 039 + 040 STO 0 041 GSB (i) 042 STO B 043 RCL D 044 - 045 RCL C 046 ÷ 047 RTN 048 *LBL C f(x). 049 STO 0 050 GSB (i) 051 RTN 052 *LBL D Store a. 053 X⇔Y 054 STO 0 b-a. 055 - 056 X⇔Y Store n. 057 STO B 058 ÷ 059 STO C (b-a)/n 060 2 061 ÷ (b-a)/2*n 062 STO + 0 063 0 Set integral sum at 0. 064 STO 9 065 RCL B Put number of intervals in I. 066 X⇔I 067 *LBL 7 068 X⇔I Return number of intervals in I. 069 STO B 070 RCL 0 071 GSB (i) F'(R0) 072 RCL C 073 STO + 0 R0 + (b-a)/n 074 × 075 STO + 9 076 RCL B Decrement n and save function in display. 077 X⇔I 078 DSZ I 079 GTO 7 Store function number. 080 STO I 081 RCL 9 Display result of integration. 082 RTN 083 *LBL E Use numerical differentiation to generate 084 FIX xi from use guess. 085 GSB B 086 RCL B 087 GTO 0 088 *LBL 6 Evaluate f(xi) 089 RCL 0 090 GSB (i) 091 STO B 092 *LBL 0 093 RCL A Secant method calculates correction for 094 RCL 0 x value and sets values for next loop. 095 STO A 096 - 097 RCL D 098 RCL B 099 STO D 100 - 101 ÷ 102 × 103 STO - 0 Subtract Correction. 104 RCL 0 105 F0? Pause and display root if flag set? 106 PAUSE 107 ÷ RND(change/xi+1) 108 RND 109 X≠0? Accurate to display? 110 GTO 6 111 RCL 0 If it is, display result. 112 RTN 001 *LBL 1 Graphical evaluation subroutine. 002 R/S 003 RTN 004 *LBL 2 005 RAD 006 TAN f(x) = tan(x) - Inv(x) - x 007 LST X 008 - 009 RCL 2 010 - 011 DEG 012 RTN 013 *LBL 3 014 RAD 015 SIN 016 RCL 1 f(θ) = 1/√(1-k2sin2θ) 017 × 018 X2 019 1 020 X⇔Y 021 - 022 √x 023 1/X 024 DEG 025 RTN
R0 x R9 integral A xi-1 B f(xi) C Δx D f(xi-1) E Δx I function
![]() Go back to the software library
Go back to the software library
![]() Go back to the main exhibit hall
Go back to the main exhibit hall