This program was written by Guillermo Castarés and is used here by permission.
This program is supplied without representation or warranty of any kind. The author and The Museum of HP Calculators therefore assume no responsibility and shall have no liability, consequential or otherwise, of any kind arising from the use of this program material or any part thereof.
If you have comments about the program, please write to gcasta@hotmail.com.
The program solves an electric circuit of several nodes or several loops, and works with AC using complex matrix representation of the circuit. It solves DC problems as a subgroup of AC problems.
The circuit has to be specified in an ASCII file, and stored in the extended memory of the calculator. The program reads this file and prepares a complex matrix. This matrix is solved by the PVT program of the Math Module used as subroutine. Finally the program shows a complex vector with the results.
This method of entering data allows the user to modify single parameters or components in a circuit and solve the new circuit without having to enter all the data again! Also it's possible to store different circuits to solve in the extended memory.
The only limit to the number of elements in the circuit is the memory size of the circuit description file. The elements can be specified freely sorted, or with no sort at all.
Another user friendly item of the program is that the user don't need to care about the number of program and data registers (assuming there are a minimum of 15 assigned). The nice "PSIZE" function allows the program to do that.
The program accepts all R or G=1/R, X or B=-1/X, Z or Y=1/Z as well as C and L instead of X.
The program was develop for a HP-41CX with Math module.
It's also possible to use it in a HP-41CV with the X-Functions module and Math module. In this case could be useful have a little editor program to edit the ASCII file in the extended memory, used as input data, because the "ED" editor of HP-41CX will not be there.
I think should be possible too, to copy the "PVT" program from de Math module to use as subroutine when the module is not inserted. Of course this will limit the size of memory available to solve complex circuits.
With the three program routines (EEA, VELS, IELS) loaded in memory, is possible to solve problems up to six Loops/Nodes. With only two program routines (EEA & VELS or EEA & IELS) loaded in memory, is possible to solve problems up to seven Loops/Nodes.
The following table shows the number of data register required, according with the number of Nodes/Loops of the circuit:
Loops/Nodes |
Data Registers |
Elapsed Time to solve* |
1 |
23 |
1' 30" |
2 |
39 |
2' |
3 |
63 |
3' |
4 |
95 |
4' 30" |
5 |
135 |
6' |
6 |
183 |
8' 30" |
7 |
239 |
12' |
(* Approximated. This elapsed time depends on the number of components.)
The program solves circuits by Nodes Voltages and Loops Currents methods. In the first case, only Current Sources are allowed, in the second case only voltage Sources are allowed. If you have to solve a circuit with mixed sources types, then you have to convert all of them to the same type before to solve the circuit.
The circuit is described in an ASCII file in the extended memory. The name of the file can be freely chosen.
The following elements are allowed:
Symbol |
Component type |
V |
Independent Voltage Source |
I |
Independent Current Source |
R |
Resistance |
G |
Conductance |
L |
Inductance |
C |
Capacitance |
X |
Reactance |
B |
Susceptance |
Z |
Impedance |
Y |
Admittance |
The following elements have only one parameter: R, G, L, C, X, B. The following elements have two parameters expressed as a complex number in rectangular form: Z, Y, V, I.
The values of the parameters should be expressed according to the flags 28 and 29 (decimal symbol and digit groups). Here we assumed that flag 28 is "Clear" and flag 29 is "Set".
The first step is to decide if we will solve a Loops Currents problem or a Nodes Voltages problem.
Loops currents
Identify all the independents loops of the circuit and number them beginning from 1 (one). All the currents are supposed clockwise. In consequence, in each branch (component connecting two nodes) the two currents have opposite courses.
If a component belongs to a only independent loop, then it's described as belonging to a fictitious loop identified by 0 (zero) (non independent).
Only voltage sources are allowed. The polarity of them have to be according to the current in the loop
The first register of the input file is:
In
where n is the number of independent loops.
The following registers of the input file describes one component each one:
ncm par1 par2
where:
n is the number of the first loop
m is the number of the second loop
c is the component type
par1 is the value of the component or the real part of it
par2 is the imaginary part of a two parameters component. Assumed 0 if no present.
The last register of the input file is:
END
Nodes Voltages
Node is the join of more than two elements.
Identify all the nodes of the circuit and number them beginning from 0 (zero). The node numbered zero will be the reference one. The nodes numbered from 1 (one) are the independent nodes.
Only Current power supplies are allowed. Conventionally is supposed that them are sending current from the first node to the second node.
The first register of the input file is:
Vn
where n is the number of independent nodes.
The following registers of the input file describes one component each one:
ncm par1 par2
where:
n is the number of the first node
m is the number of the second node
c is the component type
par1 is the value of the component or the real part of it
par2 is the imaginary part of a two parameters component. Assumed 0 if no present.
The last register of the input file is:
END
Starting to solve
Once the file describing the circuit is ready, it is necessary to put the file name in the alpha register to call the "EEA" program:
Keystrokes: Display: [ALPHA] FileName [ALPHA] [XEQ] [ALPHA] EEA [ALPHA]
If there are capacitances or inductances in the circuit then the program will ask for the frequency.
Finally the program will show the real and imaginary parts of each current/voltage on the circuit.
To solve the following circuit we will use the voltage nodes method, because there is a current source.
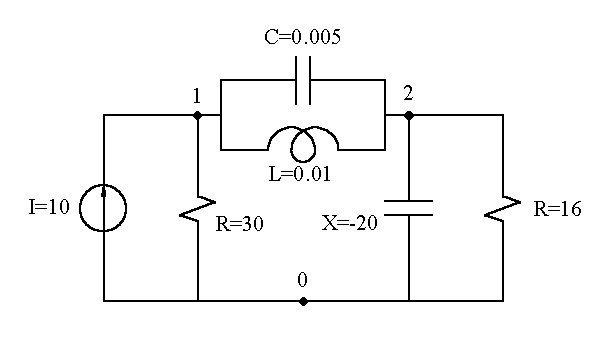
The first step is to identify the nodes and number them from 0. In this circuit there are a reference voltage node (0) and to nodes 1 and 2.
Then we have to create the file with the circuit description:
| Keystrokes: | Display: | Comment: |
|---|---|---|
| [ALPHA] CIRC1 [ALPHA] | 0,0000 | file name |
| 10 [XEQ] [ALPHA] | XEQ _ | file size |
| CRFLAS [ALPHA] | 10,0000 | create file ASCII |
| [XEQ] [ALPHA] | XEQ _ | |
| ED [ALPHA] | 00 T | invoke text editor |
| V2 [R/S] | 01 T | type of circuit and size |
| 0I1 10 [R/S] | 02 T | current source |
| 0R1 30 [R/S] | 03 T | resistance |
| 1C2 0,005 [R/S] | 04 T | capacitance |
| 1L2 0,01 [R/S] | 05 T | inductance |
| 0X2 -20 [R/S] | 06 T | reactance |
| 0R2 16 [R/S] | 07 T | resistance |
| END [R/S] | 08 T | end of file |
| [ON] | 10,0000 | exit editor |
Once the circuit is described and stored in the extended memory, we can solve it:
| Keystrokes: | Display: | Comment: |
|---|---|---|
| [ALPHA] CIRC1 [ALPHA] | 10,0000 | file name |
| [XEQ] [ALPHA] | XEQ _ | invoke the program |
| EEA [ALPHA] | 0I1 10 | shows first component |
| 0R1 30 | shows second component | |
| 1C2 0,005 | ... | |
| FREQ=? | ask for frequency | |
| 50 [R/S] | 1L2 0,01 | shows following component |
| 0X2 -20 | ... | |
| 0R2 16 | ... | |
| END | end of file | |
| V(1)X=83,7467 | V1 real | |
| [R/S] | V(1)Y=-46,7976 | V1 imaginary |
| [R/S] | V(2)X=82,5013 | V2 real |
| [R/S] | V(2)Y=-41,0423 | V2 imaginary |
| [R/S] | V(1)X=83,7467 | shows the first again... |
NONEXISTENT: The file contains a component not supported. The circuit type is "I" and contains a current source. The circuit type is "V" and contains a voltage source.
NO ROOM: There is not enough memory to solve a circuit.
FL NOT FOUND: The specified circuit file doesn't exist.
FL TYPE ERR: The specified circuit file isn't an ASCII file.
Three routines forms the whole program. The first one, "EEA", is always necessary. The second one "VELS" is only necessary to solve Nodes Voltage circuits, and the third "IELS" is only necessary to solve Loop Currents problems.
EEA program:
001 •LBL "EEA" 002 CLRG 003 CLX 004 SEEKPTA 005 GETREC 006 ATOX 007 STO 09 008 ANUM 009 2 010 * 011 STO 14 012 X^2 013 LAST X 014 2 015 * 016 + 017 15 018 + 019 SF 25 020 ARCL IND X 021 FC?C 25 022 PSIZE 023 SF 00 024 SF 01 025 •LBL 08 026 GETREC 027 AVIEW 028 ATOX 029 48 030 - 031 STO 00 032 ATOX 033 STO 07 034 ATOX 035 48 036 - 037 STO 01 038 ANUM 039 STO 02 040 ATOX 041 •LBL 09 042 ATOX 043 44 044 X<=Y? 045 GTO 09 046 CLX 047 ANUM 048 STO 03 049 CLA 050 RCL 09 051 XTOA 052 "}ELS" 053 ASTO X 054 XEQ IND X 055 FC? 00 056 GTO 07 057 FS? 02 058 XEQ 01 059 FC? 02 060 XEQ 03 061 GTO 08 062 •LBL 07 063 CLD 064 SF 02 065 SF 04 066 SF 05 067 CF 06 068 CF 10 069 XROM "PVT" 070 CF 21 071 CLX 072 SEEKPT 073 GETREC 074 ATOX 075 CLA 076 XTOA 077 40 078 XTOA 079 ASTO 09 080 RCL 14 081 X^2 082 LAST X 083 + 084 14 085 + 086 STO 00 087 •LBL 10 088 RCL 14 089 2 E3 090 / 091 1 092 + 093 STO 01 094 •LBL 12 095 RCL 00 096 RCL 01 097 + 098 STO 02 099 CLA 100 ARCL 09 101 RCL 01 102 48 103 + 104 XTOA 105 41 106 XTOA 107 "}X=" 108 ARCL IND 02 109 PROMPT 110 CLA 111 ARCL 09 112 RCL 01 113 48 114 + 115 XTOA 116 41 117 XTOA 118 "}Y=" l19 RCL 14 120 2 121 / 122 RCL 02 123 + 124 ARCL IND X 125 PROMPT 126 ISG 01 127 GTO 12 128 GTO 10 129 •LBL "FRQ" 130 FC?C 01 131 RTN 132 "FREQ=?" 133 PROMPT 134 2 135 * 136 PI 137 * 138 STO 08 139 RTN 140 •LBL 01 141 1 E-3 142 STO 05 143 •LBL 05 144 1 E-3 145 STO 06 146 •LBL 06 147 RCL 05 148 RCL 06 149 + 150 INT 151 CF 03 152 1 153 X=Y? 154 SF 03 155 RCL IND 05 156 RCL IND 06 157 XEQ 02 158 ISG 06 159 GTO 06 160 ISG 05 161 GTO 05 162 RTN 163 •LBL 02 164 ENTER^ 165 ENTER^ 166 R^ 167 ENTER^ 168 R^ 169 * 170 X=0? 171 RTN 172 CLX 173 1 174 - 175 RCL 14 176 * 177 + 178 14 179 + 180 STO 04 181 RCL 14 182 X^2 183 2 184 / 185 + 186 RCL 03 187 FS? 03 188 CHS 189 ST+ IND Y 190 RCL 04 191 RCL 14 192 2 193 / 194 + 195 RCL 03 196 FC? 03 197 CHS 198 ST+ IND Y 199 RCL 04 200 RCL 02 201 FS? 03 202 CHS 203 ST+ IND Y 204 RCL 04 205 RCL 14 206 X^2 207 LAST X 208 + 209 2 210 / 211 + 212 RCL 02 213 FS? 03 214 CHS 215 ST+ IND Y 216 RTN 217 •LBL 03 218 1 E-3 219 STO 05 220 •LBL 00 221 CF 03 222 RCL 05 223 INT 224 X=0? 225 SF 03 226 RCL IND 05 227 XEQ 04 228 ISG 05 229 GTO 00 230 RTN 231 •LBL 04 232 X=0? 233 RTN 234 RCL 14 235 X^2 236 LAST X 237 + 238 + 239 14 240 + 241 STO 04 242 RCL 14 243 2 244 / 245 + 246 RCL 03 247 FS? 03 248 CHS 249 ST+ IND Y 250 RCL 04 251 RCL 02 252 FS? 03 253 CHS 254 ST+ IND Y 255 END
VELS subprogram:
001 •LBL "VELS" 002 GTO IND 07 003 •LBL 82 004 RCL 02 005 1/X 006 STO 02 007 •LBL 71 008 SF 02 009 RTN 010 •LBL 67 011 XEQ "FRQ" 012 RCL 08 013 ST* 02 014 GTO 66 015 •LBL 76 016 XEQ "FRQ" 017 RCL 08 018 ST* 02 019 •LBL 88 020 RCL 02 021 1/X 022 CHS 023 STO 02 024 •LBL 66 025 CLX 026 X<> 02 027 STO 03 028 SF 02 029 RTN 030 •LBL 90 031 RCL 02 032 X^2 033 RCL 03 034 X^2 035 + 036 ST/ 02 037 CHS 038 ST/ 03 039 •LBL 89 040 SF 02 041 RTN 042 •LBL 73 043 CF 02 044 RTN 045 •LBL 78 046 CF 00 047 END
IELS subprogram:
001 •LBL "IELS" 002 GTO IND 07 003 •LBL 71 004 RCL 02 005 1/X 006 STO 02 007 •LBL 82 008 SF 02 009 RTN 010 •LBL 67 011 XEQ "FRQ" 012 RCL 08 013 ST* 02 014 •LBL 66 015 RCL 02 016 1/X 017 CHS 018 STO 02 019 •LBL 88 020 CLX 021 X<> 02 022 STO 03 023 SF 02 024 RTN 025 •LBL 76 026 XEQ "FRQ" 027 RCL 08 028 ST* 02 029 GTO 88 030 •LBL 89 031 RCL 02 032 X^2 033 RCL 03 034 X^2 035 + 036 ST/ 02 037 CHS 038 ST/ 03 039 •LBL 90 040 SF 02 041 RTN 042 •LBL 86 043 CF 02 044 RTN 045 •LBL 78 046 CF 00 047 END
Before PVT call:
R00 First Node/Loop of component R01 Second Node/Loop of component R02 First value/Real part of component R03 Second value/Imagine part of component R04 Used R05 Loop variable R06 Loop variable R07 ASCII code of component R08 Frequency (f) R09 ASCII code of "V" if Node Voltage or "I" if Loop Current R10 Not Used R11 Not Used R12 Not Used R13 Not Used R14 Matrix order according with PVT routine: 2*number of independent Nodes/loops R15 to 4*N^2+4*N+15 Matrix elements according with PVT routine
After PVT call:
R00 Register number of first element of matrix
R01 Loop variable to index Loop/Node number
R02 Register address of real part of result
R03 Not Used
R04 Not Used
R05 Not Used
R06 Not Used
R07 Not Used
R08 Not Used
R09 "V(" or "I(" according with the problem type
R10 Not Used
R11 Not Used
R12 Not Used
R13 Not Used
R14 Matrix order according with PVT routine: 2*number of independent Nodes/loops
R15 to 4*N^2+4*N+15 Matrix elements according with PVT routine
00 End of input file not reached 01 Frequency unknown 02 The component is not a power supply 03 Used to form the equations system XX All the flags used by PVT routine
![]() Go back to the HP-41 software library
Go back to the HP-41 software library
![]() Go back to the general software library
Go back to the general software library
![]() Go
back to the main exhibit hall
Go
back to the main exhibit hall