The Museum of HP Calculators

Volume and Area of a Polyhedron for the HP-41

This program is supplied without representation or warranty of any kind. Jean-Marc Baillard and The Museum of HP Calculators therefore assume no responsibility and shall have no liability, consequential or otherwise, of any kind arising from the use of this program material or any part thereof.

Overview

1°) Volume
2°) Volume & Area ( X-Functions module required )

-The polyhedron is defined by its n vertices V₁(x₁,y₁,z₁) , .......... , V_n(x_n,y_n,z_n) and f faces.
-Each face has to be determined by its vertices, seen counterclockwise from outside the polyhedron.

-The polyhedron is divided in several tetrahedrons and a sum of determinants of order 3 gives the volume.
-Likewise, the area is obtained by a sum of norms of cross-products.
-The position of the origin of the coordinates doesn't change the results,
and these programs also work if the polyhedron is not convex.

1°) Volume

Data Registers: • R00 = n.fff = n + f /1000 ( These registers are to be initialized before executing "PHV" )

                                  • R01 = x₁   • R04 = x₂   ..........   • R3n-2 = x_n         • R3n+1 = vertices of face 1
                                  • R02 = y₁   • R05 = y₂   ..........   • R3n-1 = y_n           ........................................
                                  • R03 = z₁   • R06 = z₂   ..........   • R3n = z_n              • R3n+f = vertices of face f

-The vertices of a face are to be coded on 2 digits from the decimal point.
-The integer part represents the 1st vertex, the fractional part represents the other ones.
-For example, 1-2-12-5 ( meaning the polygon V₁V₂V₁₂V₅ ) must be stored 1.021205

-If the face has more than 5 vertices, it must be divided into several parts:

           1*
             |         *7                          for instance, the heptagon   1-2-3-4-5-6-7 will be stored 1.020304      in a register
     2*    |                                                                                                                       and   1.04050607 in the next one ( or another one )
    3*     |             *6
          4*      5*                            another possibility is for example:   3.04050607 & 3.070102 ... etc ...

Flags: /
Subroutines: /

01 LBL "PHV"
02 CLA
03 RCL 00
04 INT
05 3.003
06 *
07 RCL 00
08 FRC
09 ISG X
10 +
11 STO N
12 LBL 01
13 RCL IND N
14 STO O
15 LBL 02
16 RCL O
17 INT
18 STO O
19 LASTX
20 FRC
21   E2
22 *
23 INT
24 LASTX
25 FRC
26 ST+ O
27   E2
28 *
29 INT
30 3
31 ST* Z
32 ST* T
33 *
34 STO Q
35 RDN
36 STO P                  ( synthetic )
37 DSE X
38 DSE Y
39 DSE Y
40 X<>Y
41 RCL IND Y          ( lines 41 to 86 add the value of a determinant to synthetic register M )
42 RCL IND Y
43 *
44 ISG Y
45 CLX
46 DSE Z
47 RCL IND Z
48 RCL IND Z
49 *
50 -
51 RCL IND Q
52 *
53 ST+ M
54 DSE Q
55 DSE Z
56 CLX
57 RCL IND Z
58 RCL IND P
59 *
60 ISG Y
61 CLX
62 DSE P
63 DSE P
64 RCL IND Y
65 RCL IND P
66 *
67 -
68 RCL IND Q
69 *
70 ST- M
71 ISG P
72 CLX
73 DSE Q
74 RCL IND Y
75 RCL IND P
76 *
77 ISG P
78 CLX
79 DSE Z
80 RCL IND Z
81 RCL IND P
82 *
83 -
84 RCL IND Q
85 *
86 ST- M
87 RCL O
88   E2
89 *
90 FRC
91 X#0?
92 GTO 02              ( a three-byte GTO )
93 ISG N
94 GTO 01              ( a three-byte GTO )
95 X<> M
96 6
97 /
98 CLA
99 END

( 164 bytes / SIZE 3n+f+1 )

STACK INPUT OUTPUT

X / Volume

Example: The polyhedron below has 11 vertices and 12 faces, so 11.012 STO 00

-The coordinates of the vertices are:

     V₁(1,1,10)    store these 3 numbers into R01 R02 R03      the 12 faces are      f₁ 1-11-4-3-2    whence   1.11040302   STO 34
     V₂(4,1,7)      -------------------------- R04 R05 R06                                    f₂   4-5-9-3         -------    4.050903       STO 35
     V₃(7,1,3)      -------------------------- R07 R08 R09                                    f₃   5-6-9            -------     5.0609           STO 36
     V₄(8,1,1)      -------------------------- R10 R11 R12                                    f₄   4-11-6-5       -------     4.110605       STO 37
     V₅(9,5,1)      -------------------------- R13 R14 R15                                    f₅   6-11-1-8-7   -------     6.11010807   STO 38
     V₆(1,10,1)    -------------------------- R16 R17 R18                                    f₆   9-6-7            -------     9.0607           STO 39
     V₇(1,8,3)      -------------------------- R19 R20 R21                                    f₇   9-7-10          -------     9.0710           STO 40
     V₈(1,5,7)      -------------------------- R22 R23 R24                                    f₈   10-7-8          -------    10.0708          STO 41
     V₉(8,5,3)      -------------------------- R25 R26 R27                                    f₉   10-8-2          -------    10.0802          STO 42
    V₁₀(5,4,8)     -------------------------- R28 R29 R30                                    f₁₀ 2-9-10          -------     2.0910           STO 43
    V₁₁(1,1,1)     -------------------------- R31 R32 R33                                    f₁₁ 3-9-2            -------     3.0902           STO 44
                                                                                                                            f₁₂ 1-2-8            -------     1.0208           STO 45
XEQ "PHV" >>>>   Volume = 197.5   ( in 56 seconds )

-This improbable solid approximately looks like this...

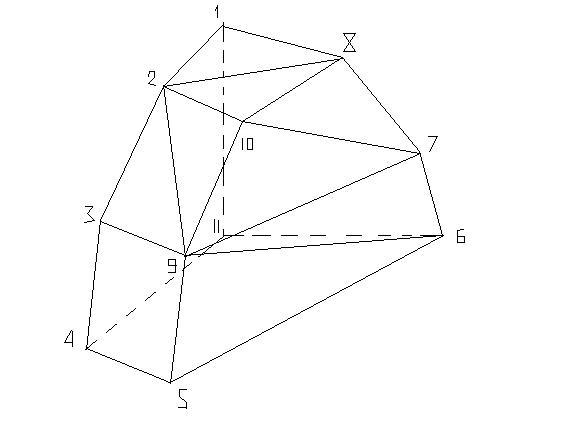
2°) Volume & Area

Data Registers: • R00 = n.fff = n + f /1000 ( These registers are to be initialized before executing "PHVA" )

                                  • R11 = x₁   • R14 = x₂   ..........   • R3n+8 = x_n          • R3n+11 = vertices of face 1
                                  • R12 = y₁   • R15 = y₂   ..........   • R3n+9 = y_n           ........................................
                                  • R13 = z₁   • R16 = z₂   ..........   • R3n+10 = z_n         • R3n+f+10 = vertices of face f

( R01 thru R09: temp - When the program stops, R10 = Volume )
Flags: /
Subroutine: "D3" ( cf "Determinants for the HP-41" )

01 LBL "PHVA"
02 CLX
03 STO 10
04 CLA                                           -If you don't want to use synthetic registers M , N , O
05 RCL 00                                        replace them by the standard registers R11 , R12 , R13
06 INT                                              replace line 04 by STO 11
07 3.003                                           replace line 12 by 14.013
08 *                                                  replace line 37 by 11.001003
09 RCL 00                                       replace lines 99 to 103 by 2 ST/ 11 RCL 11 RCL 10
10 FRC
11 +                                                 and store the coordinates and the vertices into R14 thru R3n+f+13 ( instead of R11 thru R3n+f+10 )
12 11.01
13 +
14 STO N
15 LBL 01
16 RCL IND N
17 STO O
18 LBL 02
19 RCL O
20 INT
21 STO O
22 LASTX
23 FRC
24   E2
25 *
26 INT
27 LASTX
28 FRC
29 ST+ O
30   E2
31 *
32 INT
33 3
34 ST* Z
35 ST* T
36 *
37 8.001003
38 ST+ Z
39 ST+ T
40 +
41 .003
42 ST+ Z
43 ST+ X
44 +
45 REGMOVE
46 RDN
47 REGMOVE
48 X<>Y
49 REGMOVE
50 XEQ "D3"
51 ST+ 10
52 RCL 01                    ( lines 52 to 88 add the norm of a cross-product to synthetic register M )
53 ST- 04
54 ST- 07
55 RCL 02
56 ST- 05
57 ST- 08
58 RCL 03
59 ST- 06
60 ST- 09
61 RCL 04
62 RCL 08
63 *
64 RCL 05
65 RCL 07
66 *
67 -
68 X^2
69 RCL 04
70 RCL 09
71 *
72 RCL 06
73 RCL 07
74 *
75 -
76 X^2
77 +
78 RCL 05
79 RCL 09
80 *
81 RCL 06
82 RCL 08
83 *
84 -
85 X^2
86 +
87 SQRT
88 ST+ M
89 RCL O
90   E2
91 *
92 FRC
93 X#0?
94 GTO 02             ( a three-byte GTO )
95 ISG N
96 GTO 01             ( a three-byte GTO )
97 6
98 ST/ 10
99 X<> M
100 2
101 /
102 RCL 10
103 CLA
104 END

( 168 bytes / SIZE 3n+f+11 )

      STACK        INPUTS      OUTPUTS

           Y             /          Area

           X             /        Volume

Example: With the same polyhedron, 11.012 STO 00 and store x₁,y₁,z₁ , .......... into R11 thru R55 ( instead of R01 thru R45 )

XEQ "PHVA" >>>> Volume = 197.5000 = R10 ( in 76 seconds )
X<>Y Area = 227.9981

Go back to the HP-41 software library
Go back to the general software library
Go back to the main exhibit hall