The Museum of HP Calculators The Museum of HP Calculators
In 1614, John Napier discovered the logarithm which made it possible to perform multiplications and divisions by addition and subtraction. ie:
a×b = 10(log(a)+log(b)) and a÷b = 10(log(a)-log(b))
This was a great time saver but there was still quite a lot of work required. The mathematician had to look up two logs, add them together and then look for the number whose log was the sum. Edmund Gunter soon reduced the effort by drawing a number line in which the positions of numbers were proportional to their logs.
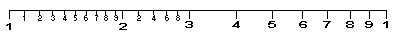
The scale started at one because the log of one is zero. Two numbers could be multiplied by measuring the distance from the beginning of the scale to one factor with a pair of dividers, then moving them to start at the other factor and reading the number at the combined distance.
Picture of a 2 foot Gunter scale (~110K) The yellow spots are brass inserts to provide wear resistance at commonly used points.
Closeup on the Gunter scale (~72K)
Soon afterwards, William Oughtred simplified things further by taking two Gunter's lines and sliding them relative to each other thus eliminating the dividers.
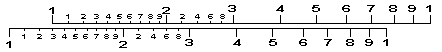
In the years that followed, other people refined Oughtred's design into a sliding bar held in place between two other bars. Circular slide rules and cylindrical/spiral slide rules also appeared quickly. The cursor appeared on the earliest circular models but appeared much later on straight versions. By the late 17th century, the slide rule was a common instrument with many variations. It remained the tool of choice for many for the next three hundred years.
While great aids, slide rules were not particularly intuitive for beginners. A 1960 Pickett manual said:
"When people have difficulty in learning to use a slide rule, usually it is not because the instrument is difficult to use. The reason is likely to be that they don't understand the mathematics on which the instrument is based, or the formulas they are trying to evaluate. Some slide rule manuals contain relatively exhaustive explanations of the theory underlying the operations. In this manual it is assumed that the theory of exponents, of logarithms, of trigonometry, and of the slide rule is known to the reader, or will be recalled or studied by reference to formal textbooks on these subjects."
A 1948 Stanley manual expressed a somewhat different opinion:
"The principles of logarithmic calculators are too well known to those likely to be interested for it to be necessary to enlarge upon the subject here, especially as it is absolutely unnecessary to have any knowledge of the subject to use the calculator"
...
"Anyone can calculate with the Fuller after a brief study of the following instructions without any mathematical knowledge whatever."
Another interesting quote from the same Pickett manual:
"A computer who must make many difficult calculations usually has a slide rule close at hand."
In 1960, "computer" was still understood to be a person who computed. By contrast, a recent dictionary begins the only definition of "computer" with "An electronic machine..."
Back to early models contents
Go on to slide rule instructions