by Rex L. James and Francis J. Yockey
IN MODEL 20 OF THE 9800 SERIES, OR MODEL 9820A, the emphasis is on using the 9800 technology to provide a highly interactive calculator. Like the 9810A, the 9820A is a ROM-driven minicomputer. Its interactive nature stems mainly from its natural algebraic language and its built-in peripherals--keyboard, printer, and display.
Modularity provides another level of interactiveness by allowing the user to configure the 9820A to fit his application.
The display consists of a single register of sixteen alphanumeric characters. Each character is formed by a seven-row, five-column matrix of light-emitting diodes (LEDs). The printer and keyboard are similar mechanically to those of the 9810A (see box, page 11).
The 9820A's combination of fast LED display and quiet thermal strip printer allows a program to be run in an interactive mode unattainable before. The hard-copy results on the printer aren't cluttered with user instructions, since these appear in the LED display. User instructions appear instantaneously in the display; there's no need to wait for a printout.
When a key is pressed a mnemonic or character appears in the display to give instant visual feedback. The 16 characters are enough so that successive keystrokes can be seen in context. For example, the expression "if the square root of B equals A, go to line 17" would require the keystrokes
IF sqrt 6 = A; GOTO 17
and would appear in the display as
IF sqrt 6 = A;GTO 17
Model 20 uses a powerful but natural instruction set to enable the user to solve complex mathematical problems quickly. The instruction set combines the features of the keyboard with the features of computer languages like ALGOL, FORTRAN, and BASIC. The result is a human-oriented, conversational approach to problem-solving, an approach that follows the structure of algebra in symbols and hierarchy.
A typical program for the 9820A is as follows. The program solves the quadratic equation (-B +/- sqrt(BB-4AC))/2A.
0: ENT "A VALUE",A 1: PRT "A = ",A 2: ENT "B VALUE", B 3: PRT "B=", B 4: ENT "C VALUE", C 5: PRT "C = ", C 6: IF 4AC>BB;GTO "IMAG" 7: PRT "REAL ROOTS";SPC 1 8: PRT (-B+sqrt(BB-4AC))/2A;SPC 1 9: PRT (-B-sqrt(BB-4AC))/2A;SPC 9;JMP -9 10: "IMAG" 11: PRT "COMPLEX ROOTS";SPC 1 12: PRT "REAL","IMAGINARY";SPC 2 13: PRT -B/2A,sqrt(4AC-BB)/2A;SPC 1 14: PRT -B/2A,sqrt(4AC-BB)/2A;SPC 9;GTO 0 15: END
Notice in lines 8 and 9 of the program that the answer to the equation is programmed in the same way that the user would write it on paper. There are no artificial machine rules to remember. To maintain the structure of algebra, implied multiplication was implemented to avoid forcing the user to insert "*" between variables to be multiplied. Parentheses can be used and nested to any depth to change the order of evaluation of an algebraic expression.
Lines 0-5 demonstrate the interactiveness of the calculator. First the calculator stops and displays an alpha message of what is to be entered. The user then keys in the desired value. After RUN PROGRAM is pressed the calculator stores the value away and prints the label and the value of the entered data. In this way all three values, A, B, and C may be entered. The roots then appear on the printout.
Convenient editing features have been included in the 9820A. To edit the above program to change to the absolute form of the GOTO, the user would key in GOTO 6 RECALL. Line 6 will be recalled to the display. Hitting the back key 7 times will give the following display:
6:IF 4AC>BB; GTO
To finish the edit, the user keys in 1 0 STORE to form the new line of program. Since the label is no longer needed in line 10, it can be eliminated by keying in GTO 1 0 RECALL DELETE. The new listing is as follows.
0: ENT "A VALUE",A 1: PRT "A = ",A 2: ENT "B VALUE",B 3: PRT "B - ', B 4: ENT "C VALUE",C 5: PRT "C = ",C 6: IF 4AC>BB;GTO 10 7: PRT "REAL ROOTS";SPC 1 8: PRT (-B + sqrt(BB-4AC))/2A;SPC 1 9: PRT (-B - sqrt(BB-4AC))/2A;SPC 9;JMP -9 10: PRT "COMPLEX ROOTS";SPC 1 11: PRT "REAL","IMAGINARY";SPC 2 12: PRT -B/2A,sqrt(4AC-BB)/2A;SPC 1 13: PRT -B/2A,-sqrt/(4AC-BB)/2A;SPC 9;GTO O 14: END
Notice that the label has been deleted and all the lines below it have been moved up and renumbered.
With the editing keys, the user can REPLACE, INSERT, or DELETE any line or character. The user observes all of the changes as they take place, by watching the alphanumeric display.
An algebraic language is easy for humans to understand and use, but is difficult for a machine to understand and execute. Take the example:
A*B + C*D (1)
When operators appear between operands as in equation 1, the precedence of the operators becomes important in the sequence of execution. Since multiply is normally assigned a higher precedence than addition, those operations associated with multiplication are performed before addition.
Equation 1 can be rewritten so that operations are executed as they are encountered:
AB*CD* + (2)
This notation is known as "Polish," or more correctly, "reverse Polish" notation.
When equation 2 is executed, operands are passed directly to a stack, which is a temporary holding area organized so that the first item into the stack will be the last item out. When a binary operator is encountered, it is applied to the top two values of the stack. The specified operation is performed and a single result is returned to the stack. Several forms of Polish notation are widely used by most desk calculators today, including the 9810A. Its main advantages are that it is easy to implement, it has fast execution speed, and it allows compact storage of programs. Its main disadvantage is that it isn't natural to the untrained user.
To take advantage of both the naturalness of the algebraic language and the speed and compactness of Polish notation, the 9820A's algebraic language is compiled into a machine language similar to the reverse Polish notation shown in equation 2. The compiler flowchart is shown in Fig. 2, along with an example showing the process of compiling the equation
A+B^(C*D/(D+F)*G).
As a string of algebraic codes is input, the compiler forms a string of machine language codes. During the compiling operation a stack is used to hold the operators and establish their order of appearance in the compiled string. All operands are passed directly to the output string while operators are put into the stack. Before an operator is placed into the stack, the stack is checked to see that all operators of greater or equal priority are first output.
Parentheses can be used to change the normal order of execution of an algebraic statement. The left parenthesis has the effect of temporarily resetting the compiler for the evaluation of the string of codes found inside the parentheses. The right parenthesis will then cause all operators in the stack to be output until a left parenthesis occurs. However, neither of the two parentheses are needed in the compiled code.
Compilers of this and more complex types have been used for years in computers. When changes to the program have to be made, the source cards or paper tape are changed accordingly and the program is recompiled. With a desk calculator, this operation is too severe a penalty to pay. Also, it isn't possible to store both the source code and the compiled code in the calculator memory at the same time. It's necessary, therefore, to reconstruct the code for editing and program listings.
The solution to this problem is the concept of the uncompiler (see Fig. 3). With the uncompiler, it's possible to take the compiled code as input and reconstruct the original algebraic form. The code is scanned backwards. Parentheses are inserted where needed in the reconstructed code, and redundant parentheses are omitted. For example,
(A*B) + (C*D)
will be reconstructed as
A*B + C*D
after going through the compile/uncompile process.
With the compile/uncompile feature, the 9820A only has to store the compiled form of the code. In the 9820A, a line of program is the basic unit used for the compiler/uncompiler and editing features. As a line of program is entered, it is stored in a buffer area and displayed in its algebraic form. When the STORE key is hit, the line of program is compiled and stored away in the program area.
When the user chooses to edit a line of program, the program line is located in memory, uncompiled into a buffer area, and displayed in its reconstructed form. Now editing can be performed, When the editing is finished, the line is compiled and once again stored in memory. To the user, the compile/uncompile process is transparent except for a slight pause while storing or recalling a line of program.
Another level of interactiveness is brought about by the modularity of the memory structure and the general-purpose minicomputer heart of the calculator. The 9820A can be configured to various applications in three ways: additional keyboard functions by read-only-memory additions, additional read/write memory, and addition of external peripherals.
There are thirty keys, arranged in three blocks of ten, available to the user to be defined for his special needs by means of plug-in ROM. Some plug-in modules provide mathematical functions, others give high-level-language control of external peripheral devices, and another allows users to define subroutines for their own special functions.
Because MOS RWM is used, additional user memory may easily be added to the basic machine. The fully loaded 9820A has 9K (9216) 16-bit words of memory: 7K is ROM and 2K is RWM.
The I/O structure provides four I/O slots on the back of the calculator to accept interface cards for peripheral devices. An I/O expander augments the 4 I/O slots of the calculator.
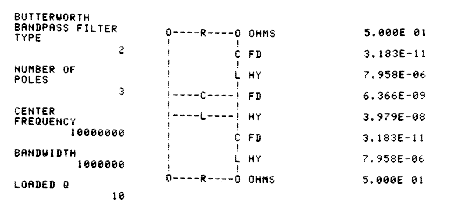
A good example of Model 20's interactive nature is this Butterworth filter design program.
Display: NUMBER OF POLES? Key in: 3 Display: CENTER FREQUENCY Key in: 10000000 Display: BAND WIDTH? Key in: 1000000 Display: RESISTANCE? Key in: 50 Display: REALIZATION TYPE Key in: 2
Realization Type 2 specifies the physical configuration of the circuit. With this input the output shown below comes from the printer.
The 9810A and 9820A Calculators use the same thermal printer and keyboard design.
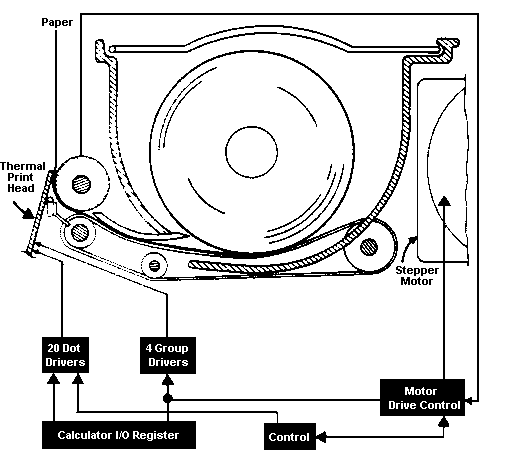
The printer (above) prints lines of sixteen alphanumeric characters on heat-sensitive paper. A five-by-seven dot matrix is used to form each character. The printer has a row of print elements distributed linearly across its printing head. Each print element is an electrical resistor of the right size and shape to produce a dot on heat-sensitive paper moved at a right angle to the line of print elements. Dots are formed in the conventional manner by exciting a resistor element with a pulse of electrical current, which raises its temperature.
The printer produces each line of print by printing the top row of all sixteen characters, then stepping down to print the second row, and so on until all seven rows are printed. Three blank steps are then added to produce the space between lines.
The printer is quiet and adaptable and has a minimum number of moving parts--all in the paper advance.
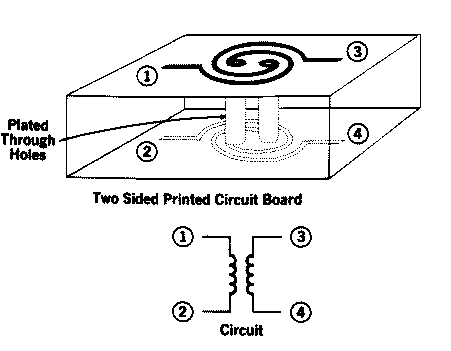
The keyboard is a contactless unit made up of an array of printed circuit transformers (above). The secondaries of all the coils are tied in series to form the sense line (below). The primaries of the coils are arranged in pairs. Each pair is connected in series with opposite polarity. Every pair has a drive and sink line, which is selected and driven by the scanner.
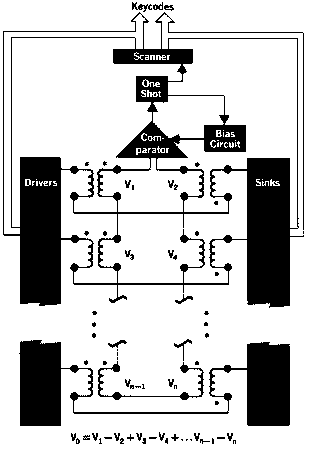
Centered above each coil is a metal disc attached to the end of the key shaft. When a key is pressed the disc moves closer to the coil. The disc acts like a shorted turn, reducing the coupling of the coil and unbalancing the pair. This unbalance is amplified by the comparator when it is greater than the "on" bias. The comparator triggers the one-shot multivibrator, which turns off the scanner and lowers the "on" bias. The scanner remains in the same state, which corresponds to the drive and sink line of the key that was pressed. This state is the keycode of the key pressed.
When the key is released a spring retracts the key and disc. When the unbalance is less than the lowered "on" bias the comparator turns off and the scanner starts again, ready for a new keystroke. The two bias levels give the key mechanical hysteresis.
Francis J. Yockey
Frank Yockey developed the interactive firmware and the peripheral control ROM blocks for the 9820A. A University of Michigan graduate with B.S.E.E. (1964) and M.S.E.E. (1965) degrees, Frank came to HP in 1965. His first design contributions were to the 5480A Signal Averager and related products. He's now in calculator market development. Frank is an amateur photographer and a backpacker. He also enjoys bicycling and making (and presumably drinking) his own wine.
![]() Go back to the HP Journal library
Go back to the HP Journal library
![]() Go back to the main exhibit hall
Go back to the main exhibit hall