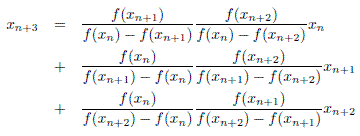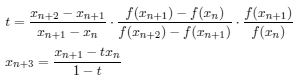HP Forum Archive 20

[ Return to Index | Top of Index ]

Lyuka and the Ostrowski method's for Root Seeking Message #1 Posted by Namir on 19 Aug 2011, 2:44 p.m. A few threads back Hugh Steers pointed out a method for finding the roots of a nonlinear function by Russian mathematician Ostrowski. I checked Luyka's web page which discussed that method and presented the code for the algorithm. It did real well. I further searched the Internet for articles about root-seeking method based on Ostrowski's method. I found several articles that further accelerated the convergence for that algorithm. A few articles were published by Chinese mathematician Zou (and colleagues) and offer somewhat elaborate enhancements to Ostrowski's method. These enhancements can solve for a root in TWO iterations (requiring 9 function calls) as compared to 6 iterations (and 12 function call) with Newton's method!. The fast Halley's method required 3 iterations and 9 function calls. The basic Ostrowski method took 3 iterations and 7 function call. So thank you Lyuka for pointing me to Ostrowski's method. I really enjoyed learning about it and about its variants. More gems in the root-seeking toolbox. Just when I thoght I learned about all the algorithms available, I get to learn about new and even more efficient ones!! Namir

Re: Lyuka and the Ostrowski method's for Root Seeking Message #2 Posted by Lyuka on 20 Aug 2011, 11:03 a.m., in response to message #1 by Namir Hi, The Ostrowski's method is a kind of root finding algorithm that uses reverse-interpolation to approximate the root. So, any other interpolation, such as Lagrange interpolation, can be used as a root finding algorithm. If you use that of n=3, a recurrence equation can be used instead of Ostrowski's This can be tested replacing a line in _ost.c Quote: t = (h * a - b) / (h - 1.0); by Quote: t = a * e * f * (f - e) - b * d * f * (f - d) + c * d * e * (e - d); t /= (f - e) * (f - d) * (e - d); Though the convergence of the method shown above is almost quadratic (order of about 1.8) for a zero of multiplicity 1 in a neighborhood of the zero, it's NOT recommended as it tends to diverge when the guess is not near the zero. IMHO, the most important thing as a root finding algorithm is not the order of convergence, but the stability of convergence, i.e. ability to find a root with very few chance of divergence. Regards, Lyuka

[ Return to Index | Top of Index ]

Go back to the main exhibit hall