The Museum of HP Calculators

HP Forum Archive 20

[ Return to Index | Top of Index ]

Solving a cubic equation using trigonometry
Message #1 Posted by Thomas Klemm on 22 Mar 2011, 4:57 a.m.

A while ago I've posted a program that uses ACOSH to solve a quadratic equation:

Short Quadratic Solver (HP-42S) Message #29

Recently I stumbled across a way to solve a cubic equation using trigonometry. Some of you might find that interesting as well.

Cheers
Thomas

Equations

A general cubic equation can be transformed to the following form using a substitution:

The trick is to use the following identity:

Here we set:

With the following substitution we can get a closed-form solution:

A similar formula can be found using the following identity:

Programs

 00 { 31-Byte Prgm }           00 { 34-Byte Prgm }
 01>LBL "CuEq"                 01>LBL "CuEqH"
 02 2                          02 2
 03 /                          03 /
 04 X<>Y                       04 X<>Y
 05 -3                         05 3
 06 /                          06 /
 07 /                          07 /
 08 LASTX                      08 LASTX
 09 SQRT                       09 SQRT
 10 /                          10 /
 11 LASTX                      11 LASTX
 12 X<>Y                       12 X<>Y
 13 ASIN                       13 ASINH
 14 3                          14 3
 15 /                          15 /
 16 SIN                        16 SINH
 17 *                          17 *
 18 2                          18 -2
 19 *                          19 *
 20 END                        20 END

Examples

x3 + 6x - 2 = 0

CuEq:    3.27480002074E-1 i0
CuEqH:   3.27480002074E-1

x3 + 3x - 4 = 0

CuEq:    1 i0
CuEqH:   1

References

Cubic Formula

Edited: 22 Mar 2011, 12:51 p.m. after one or more responses were posted

      
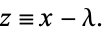Re: Solving a cubic equation using trigonometry
Message #2 Posted by Paul Dale on 22 Mar 2011, 5:23 a.m.,
in response to message #1 by Thomas Klemm

Thomas,

Very nice.

Worthy of an article?

- Pauli

      
Re: Solving a cubic equation using trigonometry
Message #3 Posted by x34 on 22 Mar 2011, 5:36 a.m.,
in response to message #1 by Thomas Klemm

Doesn't general cubic equation contain a squared element also?

            
Re: Solving a cubic equation using trigonometry
Message #4 Posted by Thomas Klemm on 22 Mar 2011, 6:18 a.m.,
in response to message #3 by x34

cf.Cubic Formula

Quote:
To solve the general cubic (1), it is reasonable to begin by attempting to eliminate the a2 term by making a substitution of the form .

This leads to formulas for p and q based upon ai.

Cheers
Thomas

            
Re: Solving a cubic equation using trigonometry
Message #5 Posted by Frido Bohn on 24 Mar 2011, 3:26 a.m.,
in response to message #3 by x34

Quote:
Doesn't general cubic equation contain a squared element also?

Indeed, the presented formula shows a "depressed cubic".

      
Re: Solving a cubic equation using trigonometry
Message #6 Posted by Crawl on 22 Mar 2011, 7:47 a.m.,
in response to message #1 by Thomas Klemm

By the way, this was the basis for HP15C minichallenge: Impossibly Short

            
Re: Solving a cubic equation using trigonometry
Message #7 Posted by Thomas Klemm on 22 Mar 2011, 11:40 a.m.,
in response to message #6 by Crawl

Thanks for pointing that out. The challenges of this forum are always a marvelous source of inspiration. However here's my source:

Mathematical Omnibus: Thirty Lectures on Classic Mathematics
Dmitry Fuchs, Serge Tabachnikov

Chapter 2. Equations
Lecture 4. Equations of Degree Three and Four

Though I haven't read the whole book yet I can only recommend it.

Best regards
Thomas

      
Re: Solving a cubic equation using trigonometry
Message #8 Posted by Namir on 22 Mar 2011, 8:56 a.m.,
in response to message #1 by Thomas Klemm

Last fall I spent much time studying the solution of polynomials, from cubic and up. I spent a lot time looking at the algorithms that solve general cubic polynomials. I used Matlab as the primary tool and then attempted to port solutions to Excel VBA and the HP41C.

I came to the conclusion that to solve cubic polynomials you best need a tool that automatically handles complex numbers. Matlab does that well and the graphing HP calculators too (although I only used PROOT to do that and wrote about it in the HP's SOLVE newsletter). The HP-42S is probably useful. J.M. Baillard has developed really cool HP41C programs that solve for the roots of polynomials (with real and complex coefficients. You can find them on this web site's HP41C program library section.

Namir

            
Re: Solving a cubic equation using trigonometry
Message #9 Posted by Ángel Martin on 22 Mar 2011, 5:02 p.m.,
in response to message #8 by Namir

Quote:
I came to the conclusion that to solve cubic polynomials you best need a tool that automatically handles complex numbers

Like the 41Z module perhaps? :-)

Well, notwithstanding all the references you mention (well worthy of their effort) the 41Z includes ZPROOT, adapted from Valentin Albillo's original program for the 41.

Cheers, 'AM

                  
Re: Solving a cubic equation using trigonometry
Message #10 Posted by Namir on 23 Mar 2011, 12:04 a.m.,
in response to message #9 by Ángel Martin

And the 41Z module too!!!

:-)

Namir

      
Re: Solving a cubic equation using trigonometry
Message #11 Posted by Eddie W. Shore on 26 Mar 2011, 5:42 p.m.,
in response to message #1 by Thomas Klemm

We can combine this with a synthetically dividing the cubic equation by the root and then use the quadratic formula to find the other two roots.

Very nice.

[ Return to Index | Top of Index ]

Go back to the main exhibit hall